Решение систем линейных уравнений по формулам Крамера. Теорема.Система n уравнений с n неизвестными, определитель которой отличен от нуля, всегда имеет решение и притом единственное

Теорема. Система n уравнений с n неизвестными, определитель которой отличен от нуля, всегда имеет решение и притом единственное. Оно находится следующим образом: значение каждого из неизвестных равно дроби, знаменателем которой является определитель системы, а числитель получается из определителя системы заменой столбца коэффициентов при искомом неизвестном на столбец свободных членов.

Пусть дана система n линейных уравнений с n переменными:

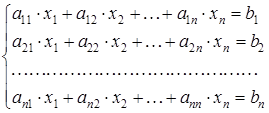
Из коэффициентов при неизвестных составим матрицу А, из свободных членов - матрицу В, т.е.

,

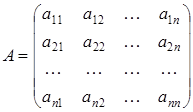Определитель матрицы А обозначим 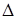и назовем определителем системы.

Таким образом,

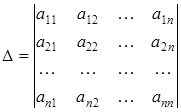
Пусть 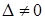. Если в определителе системы заменить поочередно столбцы коэффициентов при х ₁, х ₂,… х _n на столбец свободных членов, то получим n определителей (для n неизвестных)

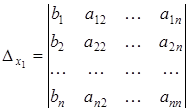
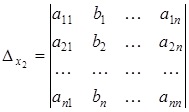
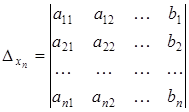
Тогда формулы Крамера для решения системы n линейных уравнений с n неизвестными запишутся так:

, ,…

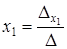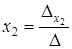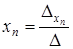
Рассмотрим случай, когда определитель системы равен нулю. Здесь возможны два варианта:

1) 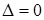и каждый определитель 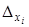равен нулю. Это возможно только тогда. когда коэффициенты при неизвестных х_i пропорциональны. Тогда система имеет бесчисленное множество решений.

2) 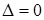и хотя бы один из определителей 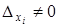. Это возможно только тогда, когда коэффициенты при всех неизвестных, кроме х_i, пропорциональны.

При этом получается система из противоречивых уравнений, которая не имеет решений.

Примеры:

1) Решить систему уравнений по формулам Крамера

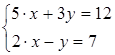
Решение:

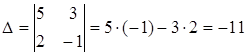
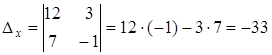
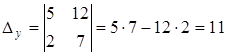
Тогда

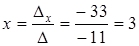
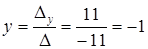
Ответ: (3; - 1)

2) Решить систему уравнений

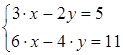
Решение:

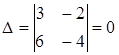
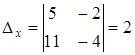
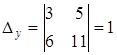
Т.к. 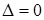, а 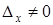, , 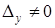то система не имеет решений

Ответ: решений нет.

3) Решить систему уравнений

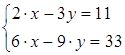
Решение:

, ,

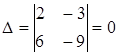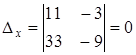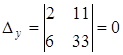
Коэффициенты при неизвестных пропорциональны, данная система имеет бесчисленное множество решений.

Ответ: бесчисленное множество решений.

4) Решить систему уравнений

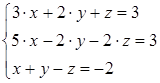
Решение:

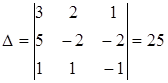
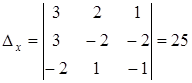
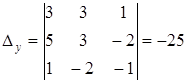
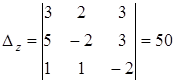
Тогда

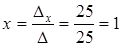
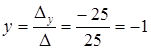
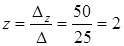
Ответ: (1; - 1;2).

Дата добавления: 2014-12-17