Основные понятия. Основными понятиями в теории вероятностей являются понятия события и вероятности события

ТЕМА 9. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТИ

Основными понятиями в теории вероятностей являются понятия события и вероятности события.

Под событием понимается такой результат эксперимента или наблюдения, который при реализации данного комплекса условий может произойти или не произойти.

События будем обозначать буквами А, В, С,... Если событие неизбежно произойдет, то оно называется достоверным, если же оно не может произойти - невозможным.

Если событие А может произойти, а может и не произойти, то оно называется случайным.

Событие, состоящее в наступлении хотя бы одного из событий А и В, будем называть суммой (объединением) событий А и В и обозначать А + В или
A 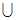В.

Событие, состоящее в наступлении обоих событий А и В, будем называть произведением (совмещением) событий А и В и обозначать АВ или А 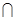В.

События называются несовместными, если появление одного из них включает появление других событий в одном и том же испытании.

Пусть, например, нас интересует появление определенного числа очков на грани при одном бросании игральной кости: i = 1,2,3,4,5,6. Выпадение конкретного числа очков назовем элементарным событием (исходом), которое обозначим 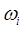. Таким образом, для каждого связанного с этим опытом события А можно выделить совокупность тех элементарных исходов 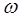, наступление которых влечет за собой наступление события А.

Пусть событие А состоит в появлении нечетного числа очков на грани. Этому событию благоприятствуют элементарные события 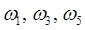т.е. некоторое подмножество множества всех элементарных исходов .

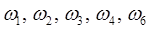Элементарные события взаимно исключают друг друга и в результате данного опыта обязательно произойдет одно из них. Пространство элементарных событий образует так называемую полную группу попарно несовместных событий, так как появление хотя бы одного из событий полной группы есть достоверное событие.

Два несовместных события, образующих полную группу, называются противоположными. Для противоположных событий одновременно выполняются два условия: А + 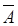- достоверное событие и 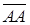- невозможное событие.

Для количественной оценки возможности появления случайного события А вводится понятие вероятности.

Вероятностью события А называют отношение числа m исходов, благоприятствующих этому событию, к числу n всех равновозможных несовместных элементарных исходов, образующих полную группу:

Р(А) = m/n

В рассмотренном примере вероятность выпадения грани с нечетным числом очков составляет Р(А) = 3/6 = 1/2.

К числу основных понятий теории вероятностей также относится частота события, под которой понимают отношение числа испытаний, в которых это событие произошло, к общему числу фактически произведенных испытаний. Частоту события называют статистической вероятностью. Для вычисления частоты события необходимо произвести в действительности испытания (опыт), что не требуется для определения вероятности.

Дата добавления: 2014-12-17