Пример 4

Пример 3.

Пример 2.

У продавца на рынке 60 арбузов, из которых 50 спелых. Покупатель выбирает 2 арбуза. Какова вероятность того, что оба выбранных арбуза спелые? (Событие А).

Решение.

Два арбуза из 60 можно выбрать числом способов равным 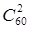. Благоприятствует событию А 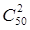шансов. Поэтому

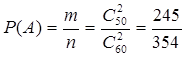
Предположим, что вероятность получить выпускнику определенную работу равна 0,4 (Р(А)), вероятность получить другую работу – 0,5 (Р(В)), вероятность получить предложения на оба места работы 0,3 (Р(АВ)). Найти вероятность получения для него по крайней мере одного из мест работы.

Решение.

Из условий ясно, что требуется найти Р(А+В). По формуле вероятности суммы двух событий:

Р(А+В)=Р(А)+Р(В)-Р(АВ)=0,4+0,5-0,3=0,6

Издательство разослало рекламные материалы на новый учебник, которые получили 80% профессоров, читающих этот курс в различных ВУЗах. Приняли ее для преподавания 30% профессоров, получивших рекламные материалы и 10% не получивших их. Чему равна вероятность того, что случайно выбранный профессор принял этот учебник для преподавания? Какова вероятность того, что профессор, принявший учебник, получил рекламные проспекты?

Решение.

Чтобы ответить на первый вопрос, надо применить формулу полной вероятности. Обозначим за событие А: учебник одобрен и принят к преподаванию.

Гипотеза Н₁: профессор не получил рекламные материалы, гипотеза Н₂: профессор не получил рекламные материалы. Очевидно, что Р(Н₁)=0,8, а Р(Н₂)=0,2, а условные вероятности Р(А/ Н₁)=0,3 и Р(А/ Н₂)=0,1. Тогда

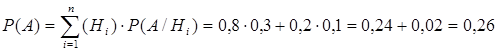
Чтобы ответить на второй вопрос, надо применить формулу Байеса, т.к. в этом случае событие А произошло (известно, что профессор уже принял учебник для преподавания).

.

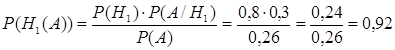Дата добавления: 2014-12-17