Пример 1

Примеры решения задач

Основные теоремы теории вероятности

Теорема сложения вероятностей двух несовместных событий:

Р(А+В) = Р(А) + Р(В)

Теорема сложения вероятностей для совместных событий:

Р(А+В) = Р(А) + Р(В)-Р(АВ)

Теорема умножения вероятностей:

а) для зависимых событий

Р(АВ)=Р(А)×Р(В/А) или Р(АВ)=Р(В)×Р(А/В)

б) для независимых событии

Р(АВ)=Р(А)×Р(В)

Формула полной вероятности:

где H₁, H₂,..., H_n гипотезы, образующие полную группу попарно несовместных событий.

Формула Бейеса:

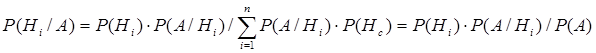
где Р (H_i/A) - вероятности гипотез

Р(А) - полная вероятность события А.

Преподаватель вызвал через старосту на обязательную консультацию трех студентов из шести отстающих. Староста забыл фамилии студентов и послал наудачу трех отстающих студентов. Какова вероятность того, что староста послал именно тех студентов, которых назвал преподаватель?

Решение.

Трех студентов из шести можно выбрать 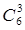способами (порядок их выбора не имеет значения). Благоприятствует событию А (вызваны именно те студенты, которых приглашал преподаватель) только один шанс. Поэтому

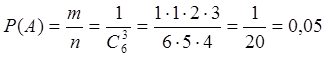
Дата добавления: 2014-12-17