
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Собственности х и торговой специализацией y, усл. ден. ед
|
|
|
|
| Форма собственности | Продовольственные товары, 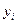
| Итого по формам собственности | ||
мясные, 
| рыбные, 
| молочные, 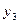
| ||
Муниципальная, 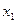
| 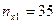
| |||
Частная, 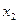
| 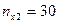
| |||
Смешанная, 
| 
| |||
| Итого | 
| 
| 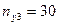
| 
|
По условию число групп обоих признаков составляет  . Распределительные частоты
. Распределительные частоты  даны в сопряженных клетках таблицы. Маргинальные частоты
даны в сопряженных клетках таблицы. Маргинальные частоты 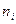 и
и 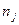 рассчитаны в итоговых строках и столбцах. По (14.а) получаем:
рассчитаны в итоговых строках и столбцах. По (14.а) получаем:

 ;
;
 .
.
Взаимосвязь качественных признаков х и у, согласно полученным значениям  и
и  , является прямолинейной и положительной, оцениваясь по шкале Чеддока для обоих коэффициентов как "умеренная". Предпочтение следует отдать коэффициенту Чупрова как учитывающему число групп s и t в вариациях признаков х и у.
, является прямолинейной и положительной, оцениваясь по шкале Чеддока для обоих коэффициентов как "умеренная". Предпочтение следует отдать коэффициенту Чупрова как учитывающему число групп s и t в вариациях признаков х и у.
Модифицированные коэффициенты Пирсона и Чупрова отличаются от предыдущих (14.а) и (14.б) использованием вместо "средней квадратической сопряженности"  показателя "общей квадратической сопряженности"
показателя "общей квадратической сопряженности"  - критерия Пирсона:
- критерия Пирсона:
а) 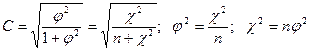 ; (15.а)
; (15.а)
б)  . (15.б)
. (15.б)
С учетом ранее найденного значения  по (15.а) получаем
по (15.а) получаем 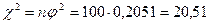 . Тогда искомые коэффициенты (15.а), (15.б) равны:
. Тогда искомые коэффициенты (15.а), (15.б) равны:
 .
.
Статистическая значимость коэффициентов сопряженности проверяется по табличному критерию  - квадрат Пирсона. Так,
- квадрат Пирсона. Так,  для уровня значимости
для уровня значимости 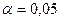 и числа степеней свободы
и числа степеней свободы  .
.
Расчетное значение этого критерия  превышает табличное
превышает табличное  , значит оба коэффициента сопряженности C и T статистически значимые.
, значит оба коэффициента сопряженности C и T статистически значимые.
Биссериальный коэффициент корреляции 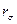 Тате предназначен для измерения тесноты связи между альтернативным признаком х и количественным признаком у.
Тате предназначен для измерения тесноты связи между альтернативным признаком х и количественным признаком у.
Исходные данные для расчета этого коэффициента содержит двумерная таблица сопряженности, имеющая две групповые строки (столбца)  для альтернативных значений
для альтернативных значений 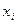 , при
, при  , и несколько групповых столбцов (строк)
, и несколько групповых столбцов (строк)  для
для 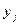 при
при  . Если признак у - интервальный, то он центрируется в виде
. Если признак у - интервальный, то он центрируется в виде

как полусумма нижнего (н) и верхнего (в) значений в группе j. Рабочее поле таблицы образуют распределенные по группам единицы наблюдения п - их частоты  с сопряженными признаками
с сопряженными признаками 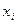 и
и 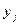 в клетке ij. Рассчитывается биссериальный коэффициент по формуле:
в клетке ij. Рассчитывается биссериальный коэффициент по формуле:
 ; (16)
; (16)
где


 - средние величины количественного признака y в альтернативных группах 1 и 2;
- средние величины количественного признака y в альтернативных группах 1 и 2;
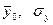 - средняя величина и среднеквадратическое отклонение признака y во всей таблице;
- средняя величина и среднеквадратическое отклонение признака y во всей таблице;
 - доли наблюденных единиц в альтернативных группах 1 и 2 соответственно с нужным и ненужным качественным признаком x;
- доли наблюденных единиц в альтернативных группах 1 и 2 соответственно с нужным и ненужным качественным признаком x;
 - табличное значение Z -распределения Фишера в зависимости от доли единиц
- табличное значение Z -распределения Фишера в зависимости от доли единиц  . Условные данные для расчета биссериального коэффициента приведены в табл. 12.8.
. Условные данные для расчета биссериального коэффициента приведены в табл. 12.8.
Таблица 12.8
Типологические группы магазинов
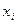
| Товарооборот 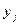 , усл. ден. ед. , усл. ден. ед.
| Итого | ||
| 150-250 | 250-350 | 350-450 | ||

| 
| 
| ||
| Продовольственные | 
| |||
| Непродовольственные | 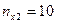
| |||
| Итого | 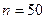
|
По (16) рассчитываем
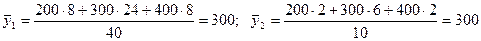 ;
;
 ;
;
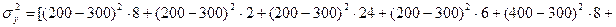
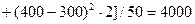 ;
;
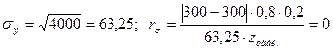 .
.
Между альтернативными группами продовольственных и непродовольственных магазинов и объемами их товарооборота отсутствует корреляционная связь. Значимость 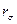 проверяется по t -критерию Стьюдента аналогично (6).
проверяется по t -критерию Стьюдента аналогично (6).
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 397; Нарушение авторских прав?; Мы поможем в написании вашей работы!