Регрессионный анализ

12.5.1. Общее представление о регрессионном анализе

После установления с помощью корреляционного анализа на­правления и тесноты связи между переменными величинами следует определить вид ее математической функции. Такая задача решается с помощью регрессионного анализа, который находит эту функцию с некоторой вероятностью по данным статистического наблюдения.

Вид функции определяется путем построения и анализа так называемого "уравнения регрессии" 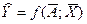, показывающего зависимость среднего значения переменной y от переменных 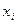, векто­ра 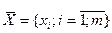и вектора параметров (коэффициентов) 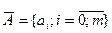, где 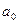- свободный член уравнения, 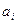, 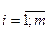- параметры (коэффициенты) факторов .

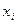Если уравнение регрессии имеет один фактор, то оно называется "парным", а если более одного - "множественным".

Уравнение регрессии сначала задается аналитически или же подбирается графически по расположению фактических данных у. После расчета своих коэффициентов и решения других вопросов оно проверяется по определенным критериям достоверности и при необ­ходимости пересматривается до получения статистически значимого результата.

12.5.2. Определение коэффициентов уравнения регрессии методом наименьших квадратов

Если математический вид уравнения регрессии выбран, то да­лее определяются его коэффициенты 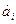. Существует несколько ме­тодов их определения. Самый распространенный - метод наимень­ших квадратов (МНК), который состоит в сведении к минимуму об­щей суммы квадратов отклонений 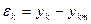фактических наблю­дений 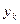от теоретических значений 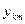путем минимизации функ­ционала:

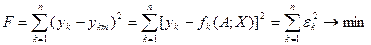. (17)

Этот функционал следует продифференцировать по искомым параметрам 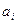, приравнять к нулю полученные выражения, упро­стить их и решить полученную систему дифференциальных уравне­ний, проверив ее, кроме того, на свою "минимальность" (во избежа­ние "максимальности") по знаку второй производной от функционала F. Решение этой системы не всегда существует и сопряжено со зна­чительными сложностями. Наиболее надежный вариант, когда берет­ся линейная функция

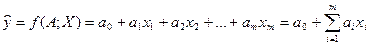. (18)

Тогда после всех математических преобразований по МНК образуется линейная "система нормальных уравнений" (СНУ), со­держащая исходные наблюдения переменных 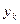и 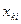и искомые ко­эффициенты регрессии :

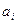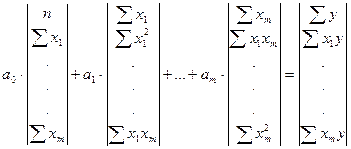. (19)

Суммирование переменных x и y производится по наблюдени­ям 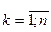, индекс которых под знаками сумм снят ради упрощения. Решение СНУ в (19) можно получить по-разному, используя метод подстановки неизвестных, метод определителей Крамера, итерацион­ный метод Гаусса-Зейделя, метод обратной матрицы и другие мето­ды, а в случае парной регрессии ее решение при 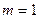получается сразу по методу прямого счета

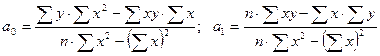. (20)

Для многомерного случая 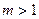факторов наилучшим методом решения СНУ является метод обратной матрицы, который позволяет получить не только наименее трудоемкое решение, но и оценить его на статистическую значимость. Матричная форма СНУ в (19) имеет вид:

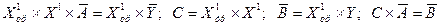, (21)

где 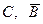- краткие обозначения соответствующих результатов.

Матрица исходных факторов 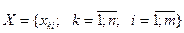, ее расширенная на первый (нулевой) единичный столбец 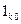матрица 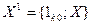и транспонированная по отношению к 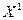матрица 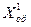имеют вид

.

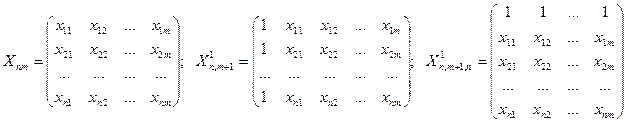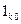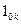Единичные элементы и при 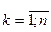в двух последних матрицах необходимы для получения первого столбца и первой стро­ки СНУ в (19), представляя собой зарезервированные места для рас­чета коэффициента .

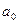Размерность исходной факторной матрицы X равна 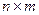, ее рас­ширенной матрицы 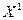- 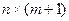, транспонированной матрицы 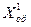- 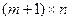, матрицы C - 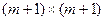, матрицы 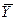- 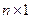, матриц 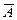и - .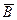

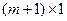Так как квадратная матрица C в левой части СНУ является симметричной относительно положительных элементов главной диа­гонали (с левого верхнего угла в правый нижний угол) и ввиду этого невырожденной, то СНУ в (19) имеет единственное решение

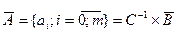. (22)

Это решение дает минимум, а не максимум функционала F в (17), так как его вторые производные, в случае линейной регрессии, - положительные величины, составляя для свободного члена 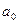вели­чину 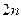и для факторных коэффициентов 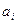- удвоенную величину положительных диагональных элементов в матрице С.

12.5.3. Линеаризация нелинейных функций

Наличие единственности решения (21) и относительная лег­кость его получения обусловливают использование линейного МНК для нелинейных функций. Поэтому до МНК нелинейную функцию стремятся по возможности привести к линейному виду относительно коэффициентов 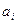. Для этого используются разные способы - услов­ная замена переменных, тейлоровское разложение сложных функций в полиномный многочлен, логарифмирование и другие приемы ли­неаризации. Например, мультипликативная степенная функция ли­неаризируется относительно параметров 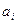, путем своего логарифми­рования:

а) ;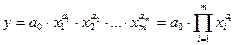

б) 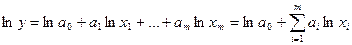. (23)

Далее в (19) образуется "скорректированная" СНУ, где все ис­ходные данные х и у будут прологарифмированы. Аналогичные "скорректированные" СНУ свойственны некоторым другим функци­ям. Так, для гиперболической и параболической функций

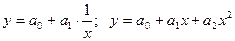, (24)

с помощью за­мены переменных из (19) получают скорректированные СНУ

а) ;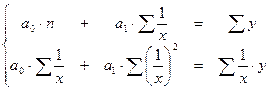

б) 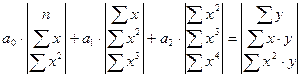. (25)

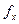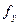Все соотношения (19) - (25) основывались на исходных несгруппированных наблюдениях. При наличии аналитической группировки или корре­ляционной таблицы в случае линейной регрессии можно также скор­ректировать все ее СНУ путем умножения переменных х и у на часто­ты и . Образуется "частотная" СНУ. Так, при 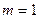для парной ли­нейной регрессии 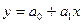и гиперболической регрессии 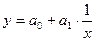их частотные СНУ имеют вид:

а) ;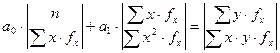

б) 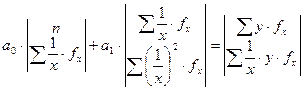. (26)

Для многомерного случая наличия более 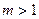разных факторов частотная СНУ уже непригодна. Надо переходить от двумерной ана­литической группировки и двумерной корреляционной таблицы к многомерным группировкам. Однако они себя практически не оправ­дывают, будучи громоздкими и трудоемкими. Поэтому лучше огра­ничиться несгруппированной СНУ (19) и действовать по общему алгоритму МНК.

12.5.4. Сравнительные показатели факторного воздействия

Основополагающей в регрессионном анализе является нестандартизованное (натуральное) уравнение регрессии с найденными по МНК коэффициентами 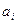, т. е. гиперплоскость

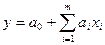. (27)

Коэффициент (свободный член) 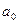- это расстояние гипер­плоскости от начала координат. Для парной регрессии при 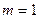та­ким расстоянием является линия среднего уровня 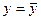, когда при 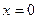образуется .

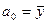Коэффициенты 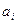, при факторах 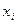(факторные коэффициен­ты) - это первые производные уравнения регрессии по переменному фактору 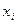. Они показывают, как в среднем изменится переменная y, если 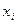изменится на одну единицу своего измерения при постоянстве других регрессионных факторов.

Свободный член 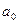измеряется в одинаковых с результатив­ной переменной y единицах. Факторные коэффициенты 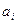, имеют смешанные единицы, измеряясь в относительных единицах перемен­ной y к фактору 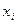. Поэтому сравнивать их между собой нельзя, как и сопоставлять по ним воздействие на у разных факторов. 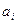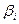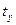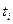Для этого надо перейти от различных коэффициентов , к безразмерным "стан­дартизованным" коэффициентам , путем построения "стандартизо­ванного (нормированного)" уравнения регрессии, которое выражает связь между нормированными отклонениями и , переменных y и ,

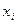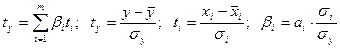. (28)

Это уравнение связано с переносом начала координат в точку пересечения средних величин .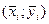

Безразмерные стандартизо­ванные коэффициенты 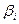показывают, на сколько своих нормиро­ванных отклонений 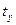изменится в среднем переменная y, если фак­тор 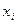изменится на одно свое нормированное отклонение 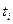, при постоянстве других регрессионных факторов. Чем больше 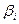, тем сильнее это воздействие, и наоборот.

Наряду с коэффициентами 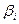для факторного сравнения рас­считываются другие показатели - коэффициенты эластичности 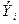вариационные коэффициенты 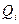, коэффициенты раздельной детер­минации 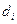, коэффициенты долевого вклада 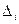и некоторые другие. В случае линейной регрессии эти коэффициенты равны

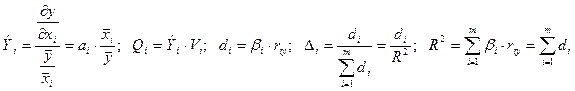, (29)

где 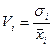- коэффициент вариации фактора 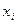, выражен­ный в долях единицы (а не в процентах). Интерпретация коэффици­ентов (29) дана далее в 12.5.7 на условном примере.

12.5.5. Статистическая адекватность уравнения регрессии

Статистическая адекватность уравнения регрессии (его досто­верность) проверяется по F -критерию Фишера-Снедекора путем рас­чета фактического значения этого критерия как соотношения фактор­ной и остаточной вариаци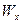й и 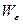в расчете на одну степень их сво­боды 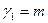и 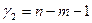, или же, как соотношение теоретических коэффициентов множественной детерминации 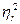и недетерминации 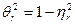в расчете на те же степени свободы 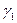и :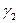

;

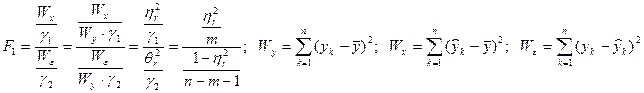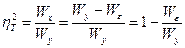, (30)

где 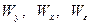- общая, факторная и остаточная дисперсии.

Преобразования в (30) основаны на правиле сложения дисперсий, которое применительно к регрессионному анализу означает, что

,

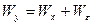и

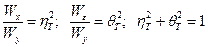при .

Теоретический коэффициент детерминации 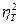показывает до­лю факторной вариации 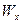в общей вариации 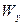. Его следует отли­чать от эмпирического коэффициента детерминации 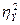, который применяется в дисперсионном анализе и показывает долю межгруп­повой дисперсии 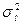в общей дисперсии 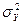, когда

;

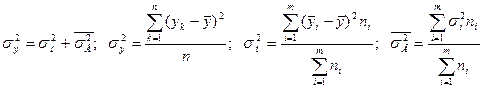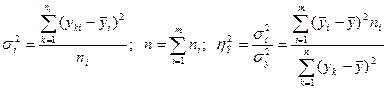, (31)

где: 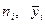- объем группы i и групповая средняя;

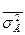- внутригрупповая дисперсия.

Корни квадратные из эмпирического и теоретического коэффи­циентов детерминации дают их соответственно эмпирическое и тео­ретическое корреляционное отношения

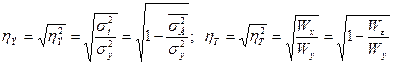. (32)

Все четыре коэффициента, 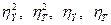изменяются от 0 до 1. Показатель 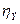служит в дисперсионном анализе мерой влияния на вариацию переменной у группировочного признака х, взятого за основание аналитической группировки, а показатель 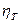является в регрессионном анализе мерой определенности (причинности) той части вариации переменной у, которая описывается уравнением регрессии. Чем адекватнее уравнение регрессии, тем 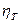больше (ближе к единице), и наоборот: чем неадекватнее уравнение, тем 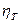ближе к нулю.

Если уравнение регрессии - линейное, то теоретический ко­эффициент множественной детерминации 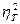превращается в сово­купный коэффициент линейной детерминации 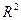. Тогда (30) прини­мает вид (7).

При 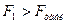уравнение регрессии считается статистически значимым (адекватным), а при 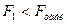- статистически незначимым (неадекват­ным).

В последнем случае вид уравнения регрессии должен быть за­менен на другой с повторением всей процедуры нового МНК. Обра­зуется "многошаговый" МНК. На этом основан "метод перебора функций ", продолжающийся до получения значимого критерия 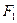и далее - до максимума .

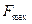Вместе с тем анализ будет усилен, если вместо 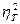и 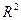ис­пользовать их корректирующие коэффициенты, применяемые в том случае, когда соотношение числа степеней свободы 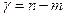и числа факто­ров т меньше своего порогового значения 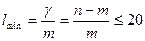. Тогда имеем

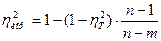; (33.а)

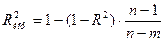. (33.6)

Подставив (33.а) в (30) и (33.6) в (7), получим 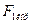и 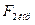. Если теперь окажется, что 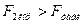, то уже есть полное основание счи­тать, что замена линейной регрессии на криволинейную была эффек­тивной.

12.5.6. Статистическая значимость коэффициентов регрессии

Выяснив вопрос об адекватности уравнения регрессии, надо определить далее значимость (достоверность) его коэффициентов, которая проверяется по t -критерию Стьюдента путем расчета его фактических значений 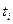как модульных отношений оцениваемых показателей 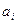, к их несмещенным ошибкам :

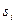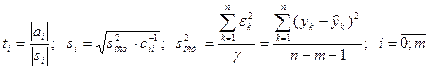, (34)

где: 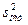- скорректированная остаточная дисперсия (квадратическая ошибка регрессии);

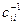- диагональный элемент обратной матрицы 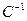в СНУ.

Если 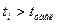, то коэффициент 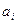считается статистиче­ски значимым с уровнем значимости 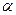и степенями свободы 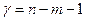, а если 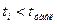- то статистиче­ски незначимым.

Незначимость коэффициента 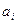означает необходимость ис­ключения из уравнения регрессии фактора 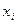, или замены его на дру­гой, ранее не рассматриваемый. Если незначимых коэффициентов несколько, то в первую очередь исключается тот, который имеет ми­нимальный долевой вклад 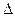или минимальный средний ранг 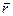по разным показателям факторной эффективности. Исключение фактора сказывается на коэффициентах 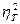и F. Если они от этого увеличи­лись, то отсев факторов был эффективен, а если не увеличились, то неэффективен.

Процедура исключения-включения факторов продолжается в многошаговом МНК до тех пор, пока все 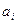, не будут значимыми. Это не всегда возможно. Тогда надо менять исходные условия: снизить уровень значимости 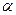; уменьшить число факторов т; увеличить число наблюдений п.

Если ни одно из этих условий или их комплекс не дает нуж­ных результатов, то следует отказаться от данного вида регрессии и перейти к другому ее виду, который допускает значимость своих ко­эффициентов при существующих условиях.

12.5.7. Условный пример регрессионного анализа

По исходным данным табл. 12.2 об объеме розничного това­рооборота у (условные денежные единицы), численности работников 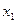(тыс. человек) и размере торговой площади 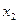(100 кв. м) в пяти магазинах проведем регрессионный анализ с помощью линейного МНК. Необходимые для двухфакторной модели подготовительные расчеты проведены в табл. 12.9.

Таблица 12.9

Дата добавления: 2014-11-29