
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расчет общей, с факторной и остаточной вариаций
|
|
|
|
| № п/п | 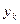
| 
| 
| 
| 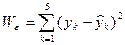
|
| 3,1 | 3,4705 | 0,8100 | 0,2804 | 0,1373 | |
| 3,1 | 3,4364 | 0,8100 | 0,3176 | 0,1132 | |
| 5,0 | 5,1254 | 1,0000 | 1,2665 | 0,0157 | |
| 4,4 | 3,6468 | 0,1600 | 0,1248 | 0,5673 | |
| 4,4 | 4,3179 | 0,1600 | 0,1011 | 0,0067 | |
| Итого | - | - | 2,9400 | 2,0904 | 0,8402 |
Расчетные значения  получены путем подстановки в уравнение регрессии факторных данных по наблюдению к. Например, для первого наблюдения при
получены путем подстановки в уравнение регрессии факторных данных по наблюдению к. Например, для первого наблюдения при  и
и  имеем
имеем
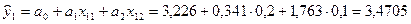 .
.
Теоретические коэффициенты множественной детерминации и корреляции (31) равны:
 .
.
Коэффициент 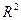 практически совпал по всем трем методам своего расчета - по методу коэффициентов корреляции (3), по методу коэффициентов раздельной детерминации (29) и по методу теоретического коэффициента детерминации (32), отличаясь численно по ним за счет округлений лишь третьей цифрой после запятой: соответственно 0,713, 0,712 и 0,711.
практически совпал по всем трем методам своего расчета - по методу коэффициентов корреляции (3), по методу коэффициентов раздельной детерминации (29) и по методу теоретического коэффициента детерминации (32), отличаясь численно по ним за счет округлений лишь третьей цифрой после запятой: соответственно 0,713, 0,712 и 0,711.
Полученный коэффициент 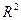 показывает, что 71,1% всей вариации товарооборота y объясняется ее линейной зависимостью от изменения факторов
показывает, что 71,1% всей вариации товарооборота y объясняется ее линейной зависимостью от изменения факторов 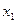 и
и 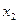 , а оставшиеся 28,9 % приходятся на долю других (не рассматриваемых) факторов или же обусловлены криволинейной связью y со своими факторами.
, а оставшиеся 28,9 % приходятся на долю других (не рассматриваемых) факторов или же обусловлены криволинейной связью y со своими факторами.
Коэффициент множественной корреляции  свидетельствует о наличии прямолинейной зависимости вариации у с совокупной вариацией факторов
свидетельствует о наличии прямолинейной зависимости вариации у с совокупной вариацией факторов 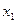 и
и 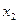 , которая оценивается по шкале Чеддока как "высокая".
, которая оценивается по шкале Чеддока как "высокая".
Для проверки значимости уравнения регрессии с помощью коэффициента 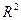 следует сначала установить, какое его значение надо использовать - исходное (теоретическое) или же скорректированное.
следует сначала установить, какое его значение надо использовать - исходное (теоретическое) или же скорректированное.
Так как  , то надо брать скорректированный коэффициент. Тогда по (33.6) и (7) получим:
, то надо брать скорректированный коэффициент. Тогда по (33.6) и (7) получим:
 .
.
При уровне значимости 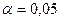 и имеющихся степенях свободы
и имеющихся степенях свободы  и
и  находим
находим  . Так как
. Так как  , то уравнение регрессии является статистически незначимым и связь между признаками подлежит замене на криволинейную.
, то уравнение регрессии является статистически незначимым и связь между признаками подлежит замене на криволинейную.
Для проверки значимости коэффициентов уравнения регрессии находим  при
при 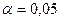 и
и  . Фактические значения этого критерия с учетом найденных диагональных элементов обратной матрицы и согласно (33) равны:
. Фактические значения этого критерия с учетом найденных диагональных элементов обратной матрицы и согласно (33) равны:

 .
.
Так как 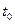 больше, a
больше, a  и
и  меньше
меньше  , то коэффициент
, то коэффициент 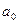 - значим, а коэффициенты
- значим, а коэффициенты  и
и 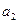 - незначимы. Незначимые факторные коэффициенты указывают на возможность отсева из уравнения регрессии соответствующих факторов. Очередность отсева целесообразно установить по значению
- незначимы. Незначимые факторные коэффициенты указывают на возможность отсева из уравнения регрессии соответствующих факторов. Очередность отсева целесообразно установить по значению  , т.е. первым должен отсеиваться фактор
, т.е. первым должен отсеиваться фактор 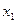 как имеющий минимальный вклад в совокупный коэффициент детерминации
как имеющий минимальный вклад в совокупный коэффициент детерминации 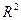 . Отсевом факторов заниматься не будем. Критерием правильности отсевов должен служить рост критерия
. Отсевом факторов заниматься не будем. Критерием правильности отсевов должен служить рост критерия 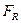 .
.
Аналогичным образом проводится регрессионный анализ для криволинейных уравнений регрессий с той лишь разницей, что в таком случае в основе будет находиться не СНУ, а система дифференциальных уравнений, которая по учебной программе не предусмотрена.
Контрольные вопросы
(выберите правильный ответ)
1. Корреляционная связь - это:
а) качественно-содержательная взаимосвязь статистических показателей;
б) функциональная зависимость переменных величин;
в) строгое соответствие вариаций переменных величин;
г) изменение переменных y в среднем при изменениях переменной 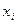 в пределах своих законов распределения;
в пределах своих законов распределения;
д) вероятностное изменение закона распределения переменной y с изменением законов распределения переменных 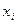 .
.
2. Главная целевая задача регрессионного анализа - это:
а) измерение тесноты связи между вариациями переменных;
б) установление направления вариаций переменных;
в) определение вида математической функции, описывающей зависимость средней величины переменной y от допустимых изменений факторных переменных 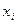 ;
;
г) расчет коэффициентов уравнения регрессии по методу наименьших квадратов;
д) оценка статистической адекватности (достоверности) уравнения регрессии по исходным данным результативного (функционального) показателя y.
3. У двух из трех предприятий совпали знаки в отклонениях переменных величин х и у, а у третьего - не совпали. Рассчитать коэффициент знаков Фехнера и указать ответ для  :
:
а) -1; б) -0,5; в) -0,33; г) 0,33; д) 0,5; е) 1.
4. Имеются абстрактные данные по двум переменным в двух наблюдениях: 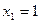 ;
; 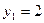 ;
;  ;
; 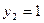 . Рассчитать парный коэффициент корреляции Пирсона и указать один ответ для
. Рассчитать парный коэффициент корреляции Пирсона и указать один ответ для 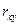 :
:
а) -1; б) -0,5; в) 0; г) 0,5; д) 1.
5. Указать допустимое значение для совокупного коэффициента линейной детерминации 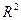 :
:
а) -2; б) -1; в) -0,5; г) 0; д) 0,5; е) 1; ж) 2.
6. Приняв исходные данные в тесте 4 за ранги переменных  и
и  , рассчитать ранговый коэффициент Спирмена и указать один ответ для
, рассчитать ранговый коэффициент Спирмена и указать один ответ для  :
:
а) -2; б) -1; в) -0,5; г) 0; д) 0,5; е) 1; ж) 2.
7. Приняв исходные данные в тесте 4 за значения четырехклеточной табл. 1. с распределением 6 единиц по двум альтернативным признакам x (строки) и y (столбцы), рассчитать коэффициент ассоциации Юла и указать один ответ для  :
:
а) -1; б) -0,5; в) -0,6; г) 0; д) 0,5; е) 0,6; ж) 1.
Таблица 1
8. Коэффициенты взаимной сопряженности Пирсона и Чупрова - это корреляции между:
а) двумя количественными признаками х и у;
б) двумя качественными признаками х и у, имеющими несколько своих состояний;
в) двумя альтернативными признаками х и y с двумя противоположными своими значениями (состояниями);
г) одним количественным и одним качественным (альтернативным) признаками;
д) безразлично какими по своему характеру признаками х и у.
9. Определить коэффициенты  и
и  в парной регрессии
в парной регрессии  , если известна система нормальных уравнений:
, если известна система нормальных уравнений:
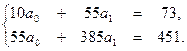
10. Коэффициент  в парной регрессии
в парной регрессии  - это:
- это:
а) эмпирическая мера тесноты связи переменных х и у;
б) эластичность переменной х;
в) вклад фактора x в парный коэффициент детерминации 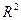 ;
;
г) показатель среднего изменения переменной y от изменения переменной х на одну свою единицу измерения;
д) соотношение темпов роста переменных y и х.
11. Если коэффициенты  ,
,  ,
,  в двухфакторной регрессии
в двухфакторной регрессии  определены по методу наименьших квадратов двумя путями - без группировки и с группировкой исходных данных, то:
определены по методу наименьших квадратов двумя путями - без группировки и с группировкой исходных данных, то:
а) их значения не зависят от метода расчета;
б) "без группировки" они больше, чем "с группировкой";
в) "без группировки" они меньше, чем "с группировкой";
г) не равны, и соотношения могут быть любыми.
12. Если в двухфакторной линейной регрессии  вариация переменной y определяется на 81% совокупным воздействием переменных
вариация переменной y определяется на 81% совокупным воздействием переменных  и
и  , то чему будет равен совокупный коэффициент линейной корреляции R:
, то чему будет равен совокупный коэффициент линейной корреляции R:
а) ±0,19; б) ±0,14; в) ±0,9; г) -0,9; д) 0; е) ±1.
13. Статистическая значимость парных коэффициентов корреляции в случае малой выборки 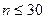 при нормальности их распределения оценивается с помощью:
при нормальности их распределения оценивается с помощью:
а) нормального закона распределения Гаусса;
б) t -распределения Стьюдента;
в) F -распределения Фишера-Снедекора;
г) Z -распределения Фишера;
д)  - распределения Пирсона.
- распределения Пирсона.
14. Исходя из перечня критериев в тесте 13, определить, какой из них применяется для оценки статистической значимости коэффициентов уравнения регрессии.
15. Исходя из перечня критериев в тесте 13, определить, какой из них применяется для оценки статистической значимости совокупного коэффициента множественной детерминации.
16. Исходя из перечня критериев в тесте 13, определить, какой из них применяется для оценки значимости коэффициентов взаимной сопряженности Пирсона и Чупрова.
17. Исходя их перечня критериев в тесте 13, определить, какой из них применяется для оценки значимости парных и чистых (частных) коэффициентов корреляции Пирсона, если они распределены не по нормальному закону.
18. Исходя из перечня критериев в тесте 13, определить, какой из них применяется для оценки адекватности уравнения регрессии.
19. Для нестандартизованного уравнения регрессии  , где
, где 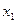 - численность работников,
- численность работников, 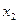 - банковская прибыль, определить, какой фактор сильнее влияет нa y, выбрав правильный ответ:
- банковская прибыль, определить, какой фактор сильнее влияет нa y, выбрав правильный ответ:
а) фактор 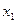 ;
;
б) фактор 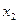 ;
;
в) одинаково;
г) нельзя сравнивать.
20. Для стандартизованного уравнения регрессии  определить аналогичный тесту 19 правильный ответ.
определить аналогичный тесту 19 правильный ответ.
21. В результате обработки  наблюдений получено криволинейное уравнение регрессии
наблюдений получено криволинейное уравнение регрессии  и определено, что общая, факторная и остаточная дисперсии равны соответственно
и определено, что общая, факторная и остаточная дисперсии равны соответственно  . Рассчитать теоретический коэффициент детерминации, фактический
. Рассчитать теоретический коэффициент детерминации, фактический 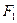 - критерий Фишера-Снедекора. Сравнить
- критерий Фишера-Снедекора. Сравнить 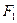 с
с  при уровне значимости
при уровне значимости 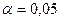 и степенях свободы
и степенях свободы  и
и 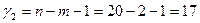 и установить, что уравнение регрессии:
и установить, что уравнение регрессии:
а) статистически значимо (адекватное);
б) статистически незначимо (неадекватное).
Список литературы
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 448; Нарушение авторских прав?; Мы поможем в написании вашей работы!