Розв’язання

Використовуємо план розв’язування задач статики:

1. тіло, що перебуває в рівновазі під дією активних (заданих) сил і реакцій опор, є балка АВ.

2. активні сили, що діють на балку, – цесила 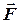і момент пари сил .

3. В’язі, що накладені на балку, – це балкові опори: у т. А – шарнірно-рухома опора, у т. В – шарнірно-нерухома опора.

4. відкидаємо в’язі та замінюємо їх дію відповідними реакціями: шарнірно-рухому опору замінюємо силою 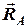, яка перпендикулярна опорній площині (землі), а шарнірно-нерухому опору – двома силами 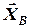і 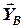. Показуємо це на розрахунковій схемі, якане змінюється ні при розв’язуванні задачі, ні після нього, тому що рівняння рівноваги сил складають саме для цієї схеми і тільки їй воно відповідає.

Реакції опор 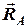, 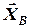і 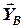є невідомими, які треба знайти у задачі.

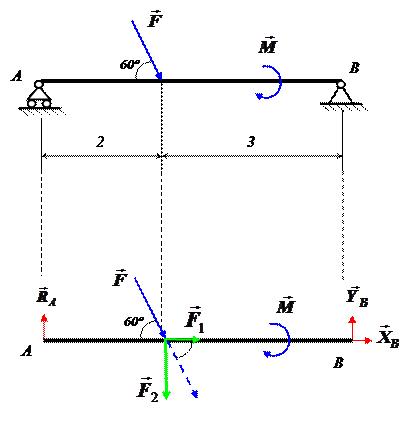Рис. 14. Розрахункова схема

Для полегшеного розрахунку розкладемо вектор сили 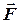на горизонтальну і вертикальну складові: 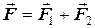. Для перевірки правильності визначення напрямків складових сил 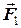і 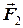їх треба скласти за правилом паралелограма сил. Якщо отримаємо задану силу 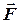, прикладену до конструкції у тій самій точці, що у первісному рисунку, то силу розкладено вірно. при цьому треба пам’ятати, що сила – вектор ковзний, тобто її можна переносити вздовж лінії її дії.

5. на балку діє плоска довільна система сил 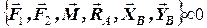, під дією якої балка знаходиться у рівновазі (стані спокою); для плоскої довільної системи сил необхідно і достатньо скласти 3 рівняння рівноваги.

6. аналізуємо статичний розв’язок задачі: кількість невідомих сил – реакцій в’язів – це 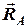, 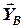і 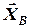, тобто їх 3, – дорівнює кількості необхідних і достатніх рівнянь рівноваги, тому задача вважається статично визначеною.

7. складаємо умови рівноваги відповідно до визначеної системи сил. намагаємось вибирати умови рівноваги таким чином, щоб у кожне рівняння увійшло тільки одне невідоме, яке з цього рівняння й визначатиме:

– сума проекцій сил на вісь х – ∑ F _{i x} = 0, з якого визначимо величину 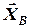;(1)

– сума моментів сил відносно т. А – ∑ М_іА = 0, з якого визначимовеличину 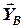; (2)

– сума моментів сил відносно т. В – ∑ М_іВ = 0, з якого визначимо величину 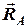. (3)

рівняння суми проекцій сил на вісь х (рівняння 1)складаємо тому, що невідом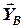і і 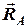,перпендикулярні до осі х, тому не ввійдуть у це рівняння, і доволі просто знайдемо .

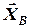при визначенні суми моментів сил відносно т. А (рівняння 2) лінії дії двох невідомих 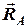і 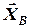перетинаються у т. А, тому їх моменти відносно т. А дорівнюють нулю, і в це рівняння увійде тільки одне невідоме 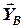. Аналогічно щодо рівняння суми моментів сил відносно т. В (рівняння 3): у т. В перетнуться лінії дії інших двох невідомих – 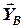і 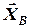, тому вони не ввійдуть у це рівняння і ми визначимо .

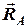8. наприкінці складемо перевірочне рівняння ∑ F_iy = 0, вяке ввійде 2 невідомих 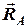і 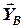; якщо у результаті отримуємо нуль, розрахунки проведено вірно.

Розрахунки

Спочатку визначимо величини складових сили :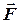

F₁= F ∙ cos60º = 2√ 3 ∙ 1/2 = √3Н;

F₂= F ∙ sin60º = 2√ 3 ∙ √3/2 = 3Н.

Покажемо ще раз усі сили, що діють на балку, щоб не пропустити ні однієї при складанні рівнянь рівноваги: .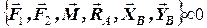

Складаємо рівняння рівноваги відповідно до умов рівноваги і розв’яжемо їх.

(1) ∑ F _{i x} = 0 │ X_В │ F₁ + X_В = 0; X _В = – F₁ = – √3Н, знак «–» указує на те, що дійсний напрямок реакції 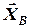протилежній указаному на схемі.

(2) ∑ М_іА = 0 │ Y_В │ – F₂ ∙ 2 – М + Y_В∙ 5 = 0; Y_В∙ 5 = F₂ ∙ 2 + М = 3 ∙ 2 + 4 = 10; Y _В = 2Н;

(3) ∑ М_іВ = 0 │ R _A │ F₂ ∙ 3 – М - R _A ∙ 5 = 0; R _A ∙ 5 = F₂ ∙ 3 – М =3 ∙ 3 – 4 = 5; R _A = 1Н.

Перевірочне рівняння

∑ F_iy = 0 │ R _A; Y_В │ – F₂ + R _A + Y_В =–3 + 1 +2 = 0 – реакції знайдено вірно.

Відповідь: X _В = – √3Н; Y _В = 2Н; R _A = 1Н.

Як бачимо, розв’язання задачі доволі просте та невелике у порівнянні з поясненням задачі. тобто навчившись розв’язувати ці задачі, їх обрахунки не займатимуть багато часу.

Приклад 2

Визначити реакції опор А і В консольної балки, якщо на неї діє рівномірно-розподілене навантаження інтенсивністю q = 0,8 кН/м.

Дані: q = 0,8 кН/м.

__________________

Визначити реакції

опор А і В балки.

Рис. 15. До прикладу 2

Дата добавления: 2014-11-29