Системы счисления. Представление данных в ЭВМ, в силу физических законов ее функционирования, не может осуществляться на основе десятичной системы счисления

Представление данных в ЭВМ, в силу физических законов ее функционирования, не может осуществляться на основе десятичной системы счисления. Базовым элементом любой цифровой ЭВМ является так называемый ключ, поведение которого характеризуется двумя состояниями – включено (1), выключено (0), то есть состояние этого ключа, а также множества других ключей в ЭВМ может быть описано с помощью двух цифр: нуля и единицы. Эти соображения послужили причиной применения двоичной системы счисления.

Все цифры в числе определяются ее порядком. Например, десятичное число 2002,9=2×10³+0×10²+0×10¹+2×10⁰+9×10^-1 можно представить в виде суммы частных произведений. Первый сомножитель принимает значение цифры в десятичной системе счисления, а второй – (число десять) основание десятичной системы счисления. Показатель степени при числе 10 равен порядковому номеру позиции цифры в исходном числе.

Для произвольной системы счисления можно записать

k × Nⁱ+k × N^i-1+…+k × N¹+k × N⁰+k × N^-1+…+ k × N^-m,

где k – принимает значение любой цифры данной системы счисления; N – основание данной системы счисления; i – номер позиции (показатель степени), которую цифра занимает в числе до запятой, а m – порядковый номер цифры в числе после запятой.

Примеры:

a) ;

b) ;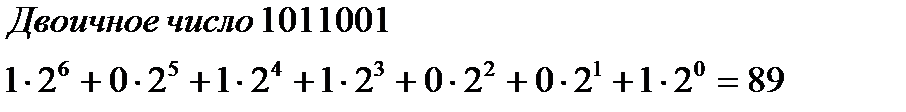

c) .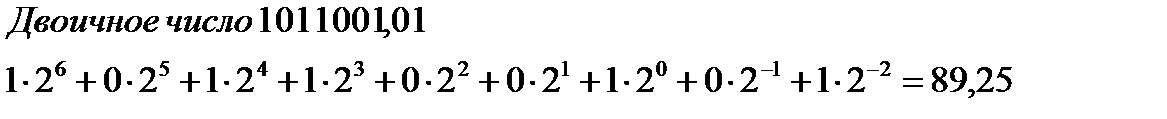

Существенным недостатком двоичной системы счисления является то, что для представления больших чисел необходимо большое количество двоичных разрядов, а это, в свою очередь, приводит к уменьшению надежности в представлении двоичных чисел. Имеется в виду, что вероятность возникновения ошибки при написании числа с увеличением его разрядности возрастает, кроме того, двоичная система счисления не является компактной. С другой стороны, отказываться от этой системы мы не можем, поэтому в качестве обоснованного компромисса используется шестнадцатеричная система счисления. Ее достоинством является компактность в записи больших чисел и простота при переходе от шестнадцатеричной системы к двоичной и обратно. В табл. 1 в первом столбце показаны десятичные числа от 0 до 15, во втором столбце двоичные эквиваленты этих десятичных чисел, а в третьем столбце приведены цифры шестнадцатеричной системы счисления.

Таблица 1

N(10)	N(2)	N(16)

Продолжение табл. 1

		A
		B
		C
		D
		E
		F

Для перехода от двоичной системы счисления к шестнадцатеричной достаточно разбить исходное двоичное число на группы по четыре цифры справа налево и затем заменить эти двоичные группы на соответствующие им цифры шестнадцатеричной системы счисления.

Например:

a) 110.0011.1100.1011.0011₍₂₎ = 63CB3₍₁₆₎;

b) 1111.0000.1010.0111₍₂₎ = F0A7₍₁₆₎;

Обратное преобразование осуществляется заменой шестнадцатеричных цифр в числе соответствующими двоичными эквивалентами из табл. 1.

Например:

2ae7b₍₁₆₎ = 0010.1010.1110.0111.1011₍₂₎.

Дата добавления: 2014-11-29