Логический элемент ИЛИ-НЕ

Логические элементы и таблица истинности

В основе всех цифровых систем лежат четыре основных логических элемента (операций):

– логическое сложение, дизъюнкция, ИЛИ;

– логическое умножение, конъюнкция, И;

– ИЛИ – исключающее;

– отрицание, НЕ;

Совокупность этих элементов обладает свойством функциональной полноты, т.е. на их основе может быть решена любая логическая непротиворечивая функция.

В электротехнических системах (рис.10) логические элементы принято обозначать в виде прямоугольников со сторонами, кратными 5мм, причем слева (как правило) показаны входы, справа – выходы.

Рис.10. Изображение логического элемента на электрических схемах

Входные величины по правилам алгебры логики обозначаются, как правило, заглавными латинскими буквами (A, B, C, …), так же обозначаются и выходные переменные. Связь между входами и выходами определяется конкретной логической функцией (рис.11.)

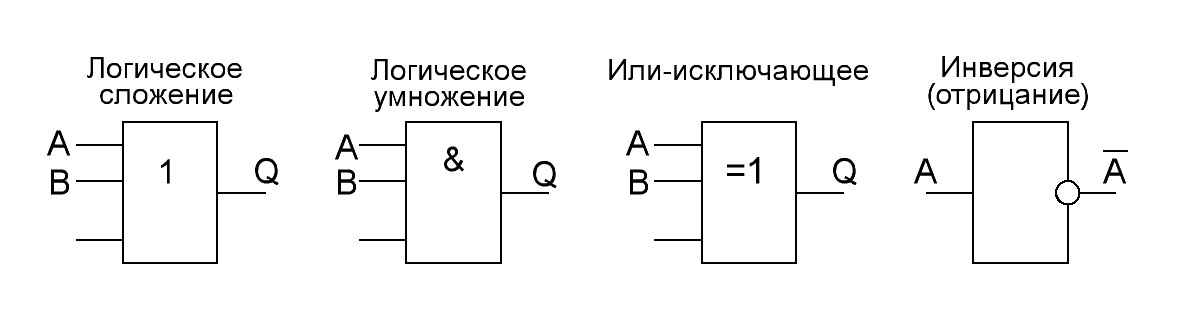
Рис.11. Изображение основных логических элементов на электрических схемах

Одним из основных инструментов для анализа цифровых комбинационных схем, построенных на этих, элементах является таблица истинности, которая состоит из N – столбцов, где N – 1 равно количеству входных переменных. А последний столбец принимает значение выходной переменной. Если количество входных переменных равно K, то количество строк в этой таблице равно 2 ^K. Важной особенностью всех входных и выходных переменных в алгебре логике является то, что все они могут принимать только два значения – нуля или единицы.

4.1. Логическое сложение, дизъюнкция, элемент «ИЛИ»

Для обозначения операции логического сложения (английское сокращенное обозначение «OR») в алгебре логики используется символ «+», например, A + B = Q.

На рис.12. показана электрическая схема, иллюстрирующая работу элемента логического сложения. Примем, что если ключ A (B) замкнут, то А (В) равно единице, и наоборот, если разомкнут, то A (B) равно 0. Если лампочка Q горит, то Q =1, если не горит, то Q =0.

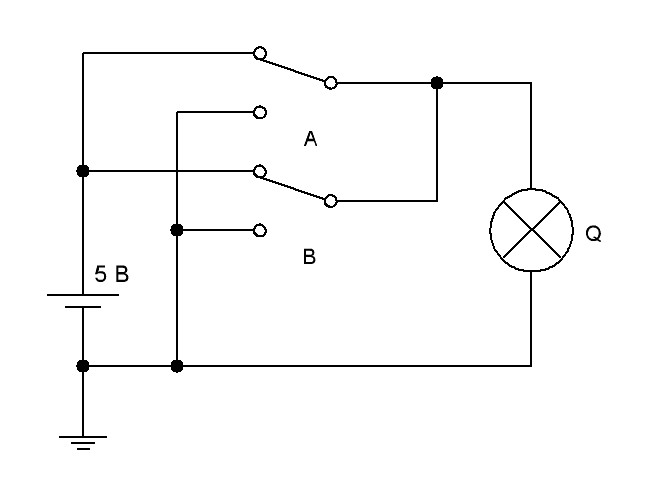
Рис.12. Электрическая схема электромеханического эквивалента логического элемента 2-ИЛИ

Из схемы очевидно следует, что если хотя бы один ключ А или В или оба ключа замкнуты, то лампочка Q горит. И только когда оба ключа разомкнуты, лампочка не горит. Эти рассуждения в формальном виде можно представить в виде таблицы истинности для логического элемента 2-ИЛИ. Цифра «2» в обозначении указывает на то, что в операции логического сложения участвует два слагаемых (в примере А и В). Табл.2 будет иметь три столбца (А, В и Q) и количество строк (за исключением заголовка таблицы), равное 2². Рассмотренную операцию можно записать в алгебраической форме следующим образом: А + В = Q.

Таблица 2

В	А	Q

Если в схеме рис.12 добавить еще один ключ С (рис.13), то работа схемы в принципе не изменится. Разница будет заключатся в том, что лампочка Q не будет гореть тогда, когда все три ключа разомкнуты. Таким образом, мы получим логический элемент 3-ИЛИ. Добавлять ключи можно сколь угодно много, при этом, очевидно, общее правило работы схемы не изменится.

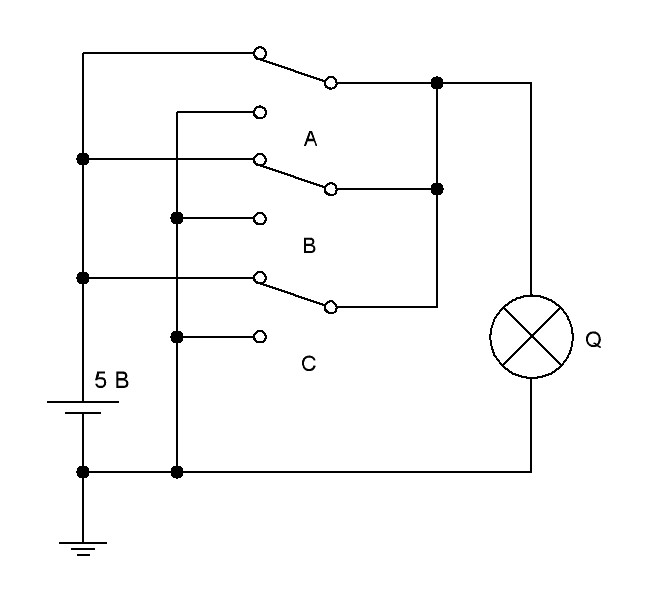
Рис.13. Электрическая схема электромеханического эквивалента

логического элемента 3-ИЛИ

Таблица истинности для логического элемента 3-ИЛИ будет состоять из четырех столбцов и иметь 2³=8 строк (табл.3).

Таблица 3

С	В	А	Q

Продолжение табл.3

Промышленность выпускает четыре типа элементов логического сложения: 2-ИЛИ, 3-ИЛИ, 4-ИЛИ и 8-ИЛИ. На схемах электрических принципиальных эти элементы изображают, как показано на рис.14.

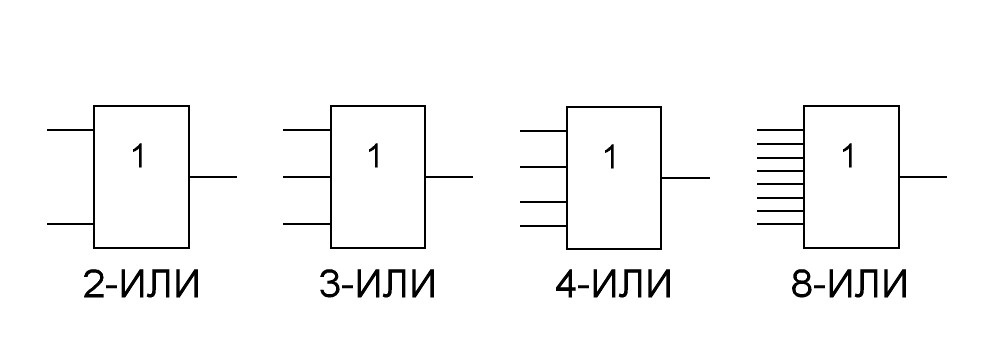
Рис.14. Условное обозначение элементов логического сложения на схемах электрических принципиальных

Все физические процессы протекают и исследуются, как правило, во времени, поэтому чтобы знать, когда и как произошло то или иное событие используются диаграммы состояний. С помощью таких диаграмм удобно исследовать и анализировать работу цифровых схем.

Для построения таких диаграмм задаются (или измеряют с помощью многоканального логического анализатора) значениями входных переменных во времени, и с помощью таблицы истинности вычисляют и строят значение выходной переменной. Например (рис.15), зададимся значениями во времени входных переменных А, В и С для логического элемента 3-ИЛИ и построим значение выходной переменной Q в каждый момент времени.

В момент времени t₁ А =1, В =1 и С =0 в четвертой строке табл.3 этому значению входных переменных соответствует значение выходной переменной Q =1. В момент времени t₂ A =0, B =0, C =0 это состояние входных переменных соответствует первой строке табл. 3, поэтому выходная переменная Q =0.

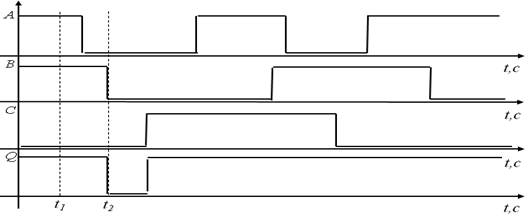
Рис.15. Диаграмма состояний для элемента 3-ИЛИ

В заключение отметим, что современные логические элементы (не только логического сложения) строятся не на механических ключах, а на так называемых транзисторных ключах. Такие ключи имеют множество преимуществ (см. стр.8). Однако нам нет необходимости «заглядывать» внутрь логических элементов, достаточно знать их таблицы истинности и различать их условные изображения в схемах.

4.2. Логическое умножение, конъюнкция, элемент «И»

В алгебре логики операция логического умножения (английское сокращенное обозначение «AND») обозначается символом умножить «·», например, А ∙ В = Q.

На рис.16. показана электрическая схема, иллюстрирующая работу элемента логического сложения.

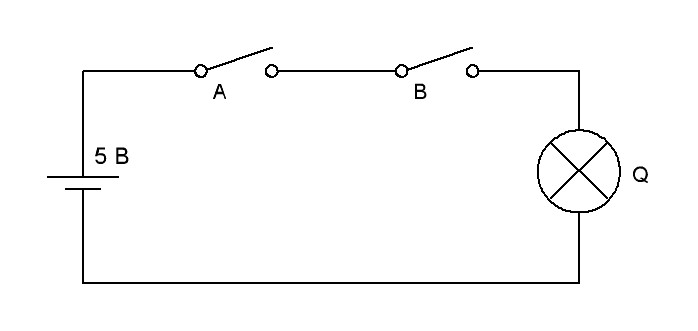
Рис.16. Электрическая схема электромеханического эквивалента логического элемента 2-И

Из схемы следует, что если хотя бы один ключ А или В или оба ключа разомкнуты, то лампочка Q не горит. И только когда оба ключа замкнуты лампочка горит. Эти рассуждения в формальном виде можно представить в виде таблицы истинности для логического элемента 2-И. Цифра «2» в обозначении указывает на то, что в операции логического умножения участвует два сомножителя (в примере А и В). Табл.4 будет иметь три столбца (А, В и Q) и количество строк (за исключением заголовка таблицы), равное 2². Рассмотренную операцию можно записать в алгебраической форме следующим образом: А ∙ В = Q.

Таблица 4

В	А	Q

Если в схеме рис.16 добавить еще один ключ С (рис.17), то правила работы схемы не изменятся. Разница будет заключатся в том, что лампочка Q будет гореть только тогда, когда все три ключа замкнуты. Таким образом, мы получим логический элемент 3-И. Добавлять ключи можно сколь угодно много, при этом очевидно общее правило работы схемы не изменится.

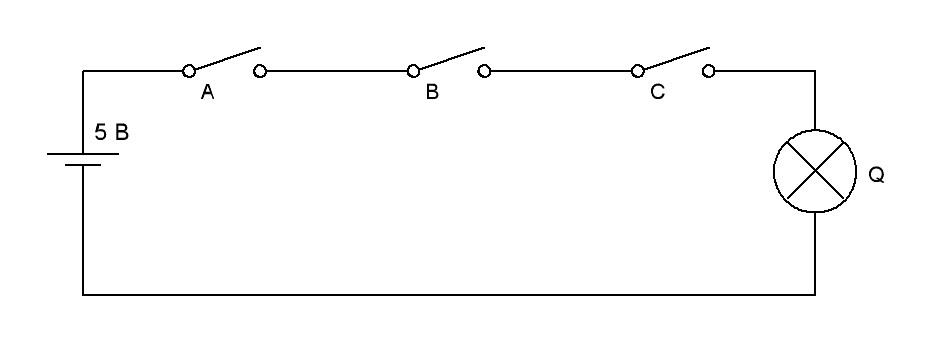
Рис.17. Электрическая схема электромеханического эквивалента логического элемента 3-И

Таблица истинности для логического элемента 3-И будет состоять из четырех столбцов и иметь 2³=8 строк (табл.5).

Таблица 5

С	В	А	Q

Промышленность выпускает четыре типа элементов логического умножения: 2-И, 3-И, 4-И и 8-И. На схемах электрических принципиальных эти элементы изображают, как показано на рис.18.

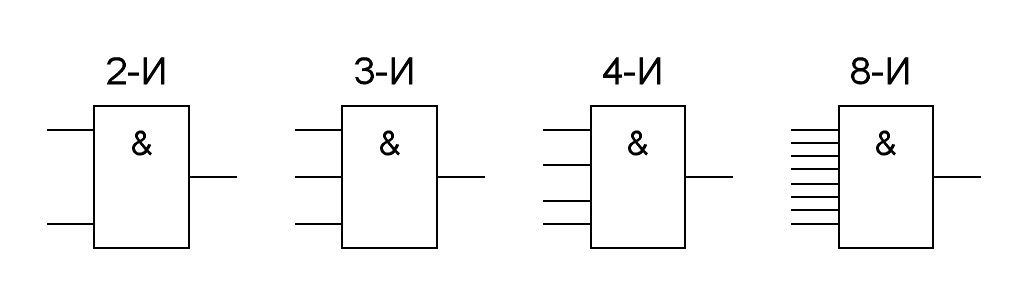
Рис.18. Условное обозначение элементов логического умножения на схемах электрических принципиальных

Построим диаграмму состояний (рис.19) для логического элемента 3-И.

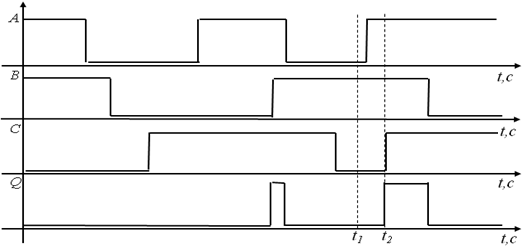
Рис.19. Диаграмма состояний для элемента 3-И

Для этого, также как и в предыдущем случае, зададимся значениями входных переменных А (t), В (t) и С (t) и в соответствии с табл.5 построим на графике значение выходной переменной Q (t). Например, в момент времени t ₁ A =0, B =1, C =0, в соответствии с значением третьей строки в табл.5 Q =0. Далее в момент времени t ₂ A =1, B =1, C =1 и в соответствии с значением восьмой строки в табл.5 Q =1.

4.3. Логический элемент «ИЛИ – исключающее»

Для обозначения этой операции в алгебре логики используют символ Å. Например, А Å В = Q. Часто для него используют английское сокращение «XOR».

Проиллюстрировать работу этого элемента с помощью механических ключей и лампочки невозможно, поэтому здесь просто необходимо знать таблицу истинности.

В табл.6 приведена таблица истинности для логического элемента 2-ИЛИ ИСКЛЮЧАЮЩЕЕ.

Таблица 6

В	А	Q

В табл.7 приведена таблица истинности для логического элемента 3-ИЛИ ИСКЛЮЧАЮЩЕЕ.

Таблица 7

С	В	А	Q

Продолжение табл.7

Промышленность выпускает четыре типа логических элементов ИЛИ ИСКЛЮЧАЮЩЕЕ: 2-ИЛИ ИСКЛЮЧАЮЩЕЕ, 3- ИЛИ ИСКЛЮЧАЮЩЕЕ, 4-ИЛИ ИСКЛЮЧАЮЩЕЕ и 8-ИЛИ ИСКЛЮЧАЮЩЕЕ. На схемах электрических принципиальных эти элементы изображают, как показано на рис.20.

Рис.20. Условное обозначение логических элементов ИЛИ ИСКЛЮЧАЮЩЕЕ на схемах электрических принципиальных

Построим диаграмму состояний (рис.21) для логического элемента 3- ИЛИ ИСКЛЮЧАЮЩЕЕ.

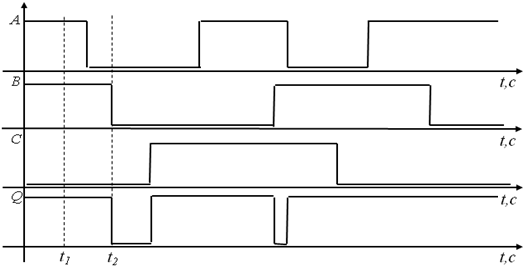
Рис.21. Диаграмма состояний для элемента 3- ИЛИ ИСКЛЮЧАЮЩЕЕ

Для этого, также как и в предыдущих случаях, зададимся значениями входных переменных А (t), В (t) и С (t) и в соответствии с табл.7 построим на графике значение выходной переменной Q (t). Например, в момент времени t ₁ A =1, B =1, C =0, в соответствии с значением третьей строки в табл.5 Q =1. Далее в момент времени t ₂ A =0, B =0, C =0 и в соответствии со значением первой строки в табл.7 Q =0.

4.4. Логический элемент отрицание, инвертор, «НЕ»

Все логические элементы, рассмотренные ранее, имели, по крайней мере, два входа и один выход. В отличие от них в схеме НЕ, часто называемой инвертором, есть только один вход и один выход. Основная функция схемы НЕ (инвертора) состоит в том, чтобы обеспечить на выходе сигнал, противоположный сигналу на входе. Условное обозначение инвертора показано на рис.22.

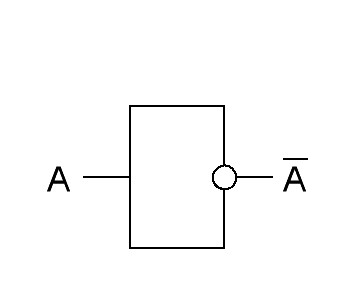
Рис.22. Условное изображение логического элемента НЕ на схемах электрических принципиальных

Если на вход А подать сигнал уровнем логической 1 (рис.23), то на выходе 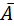получится противоположный сигнал, имеющий уровень логического нуля.

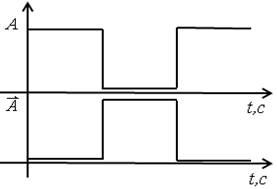
Рис.23. График сигналов на входе А и выходе 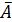логического элемента НЕ

Часто говорят, что инвертор дополняет или инвертирует входной сигнал. Черта над обозначением выходного сигнала 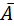указывает на то, что входной сигнал А инвертирован или взято его дополнение.

Логические элементы ИЛИ, И, ИЛИ ИСКЛЮЧАЮЩЕЕ и НЕ представляют собой четыре основных типа схем, из которых компонуются все цифровые электронные устройства. Часто для удобства и упрощения проектирования, а также изготовления цифровых систем используются множество элементов, которые в себе объединяют несколько базовых функций.

Логический элемент ИЛИ-НЕ называют также элементом отрицания ИЛИ. Это говорит о том, что для реализации функции ИЛИ-НЕ выход элемента ИЛИ должен быть инвертирован. Условное изображение логического элемента ИЛИ-НЕ показано на рис.24, а.

Рис.24. Логический элемент 2-ИЛИ-НЕ: а –условное изображение элемента 2-ИЛИ-НЕ; б –логическое выражение для выхода элемента 2-ИЛИ-НЕ

Символ инвертора (небольшой кружок) с правой стороны обозначения говорит об инвертировании результата логической операции (в данном случае логического сложения).

Таблица истинности элемента 2-ИЛИ-НЕ приведена табл.8.

Таблица 8

В	А	Q

Необходимо запомнить условное обозначение, логическое выражение и таблицу истинности для логического элемента (как, впрочем, и для всех остальных логических элементов) 2-ИЛИ-НЕ. Эти сведения часто будут нужны в Вашей работе с цифровыми электронными устройствами.

При необходимости построить диаграмму состояний для какого-либо логического элемента применяют правила, рассмотренные выше.

Дата добавления: 2014-11-29