
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общие замечания и некоторые основные определения
|
|
|
|
КРАТКИЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО ИСЧИСЛЕНИЯ
Вопросы к главе 7
1. Параметры длинной линии.
2. Эквивалентная схема длинной линии.
3. Дифференциальные уравнения длинной линии.
4. Волновая функция. Падающие и отражённые волны.
5. Первичные параметры длинной линии.
6. Вторичные параметры длинной линии.
7. Физический смысл решений дифференциальных уравнений для тока и напряжения в длинной линии.
8. Условия неискажающей длинной линии.
9. Коэффициент отражения по напряжению и току длинной линии.
10. Режим бегущих волн в длинной линии с потерями.
11. Режим бегущих волн в длинной линии без потерь.
12. Режим стоячих волн в разомкнутой длинной линии.
13. Режим стоячих волн в короткозамкнутой длинной линии.
14. Линия, нагруженная на чисто реактивную нагрузку.
15. Режим смешанных волн в длинной линии.
16. Длинная линия, нагруженная на комплексное сопротивление индуктивного характера.
17. Длинная линия, нагруженная на комплексное сопротивление емкостного характера.
ПРИЛОЖЕНИЕ
Векторное исчисление представляет собой математический аппарат, приспособленный для количественного описания физических явлений, характеризуемых величинами, которые определяются не только численными значениями, но и направлением. Будем считать, что известны основные определения скаляра и вектора, а также определение геометрических равенств, суммы и разности векторов. Подчеркнём лишь то существенное обстоятельство, что как эти основные определения, так и определения более сложных векторных операций имеют совершенно самостоятельный характер; точнее говоря, эти определения не нуждаются в привлечении какой-либо системы координат. Однако аналитическое исследование того или иного явления не может быть проведено на основании соотношений, написанных в чисто векторной символике, и приходится вводить определённую систему координат, выбор которой связан с конкретными условиями решаемой задачи.
|
|
|
Ниже приведены основные сведения из векторного исчисления, причём для аналитических соотношений применена прямоугольная декартова система координат [6].
Как известно, если три вектора  ,
, 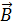 и
и 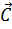 не компланарны (т. е. не параллельны в одной плоскости), то всякий вектор
не компланарны (т. е. не параллельны в одной плоскости), то всякий вектор 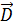 может быть представлен в форме
может быть представлен в форме
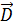 = m
= m  + n
+ n 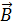 + p
+ p 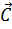 , (1)
, (1)
где m, n и p – скалярные множители, т. е. вектор может быть разложен на три составляющие, параллельные соответственно векторам  ,
, 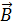 и
и 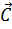 , причём единственным образом.
, причём единственным образом.
Следовательно, если в декартовой системе координат x, y и z ввести три единичных вектора 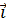 ,
, 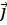 и
и 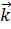 ,параллельные соответственно координатным осям x, y и z, то всякий координатный вектор
,параллельные соответственно координатным осям x, y и z, то всякий координатный вектор  в этой системе координат может быть представлен в форме
в этой системе координат может быть представлен в форме
 =Ах
=Ах 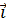 + Ay
+ Ay 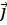 + Az
+ Az 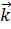 , (2)
, (2)
где Ах, Ay и Az – проекции вектора  на координатные оси.
на координатные оси.
Отметим, что будем применять так называемую правую систему координат (рис. 1), в которой положительные направления осей x, y и z совпадают с направлением соответственно большого, указательного и среднего пальцев правой руки, расположенных перпендикулярно друг к другу; иначе говоря, положительное направление оси z должно совпадать с направлением поступательного движения правого буравчика при его повороте вокруг собственной оси от оси x к оси y по кратчайшему пути.
С помощью выражения (2) получается правило геометрического сложения векторов, совпадающее с его общим определением
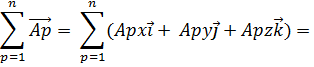
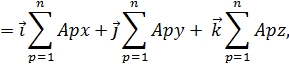
т. е. сумма векторов есть также вектор, причём
|

где
|

Скалярным произведением двух векторов  и
и 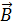 называется скаляр, равный произведению модулей А и В векторов
называется скаляр, равный произведению модулей А и В векторов  и
и 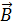 , умноженному на косинус угла θ между ними (рис. 2),
, умноженному на косинус угла θ между ними (рис. 2),
|
|
|
 ×
× 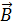 = АВ
= АВ  =АВВ=АВА, (5)
=АВВ=АВА, (5)
где Ав = А  – проекция вектора
– проекция вектора  на направление вектора
на направление вектора 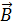 ; ВА= В
; ВА= В  – проекция вектора
– проекция вектора 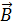 на направление вектора
на направление вектора  .
.
Векторным произведением двух векторов  и
и 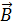 называется вектор, по величине равный площади параллелограмма, построенного на векторах
называется вектор, по величине равный площади параллелограмма, построенного на векторах  и
и 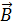 , перпендикулярный плоскости этих векторов и направленный в такую сторону, чтобы вращение от
, перпендикулярный плоскости этих векторов и направленный в такую сторону, чтобы вращение от  к
к 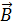 на кратчайшем пути вокруг полученного вектора происходило в ту же сторону, как вращение от оси х к оси у вокруг оси z. Таким образом, по определению (рис. 3)
на кратчайшем пути вокруг полученного вектора происходило в ту же сторону, как вращение от оси х к оси у вокруг оси z. Таким образом, по определению (рис. 3)
 ×
× 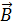 =
= 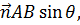 (6)
(6)
где 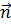 – единичный (n=1) вектор нормали к плоскости, проходящей через А и В, и направленный согласно вышеуказанному правилу (в нашем случае, когда
– единичный (n=1) вектор нормали к плоскости, проходящей через А и В, и направленный согласно вышеуказанному правилу (в нашем случае, когда  и
и 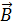 лежат в плоскости чертежа,
лежат в плоскости чертежа, 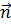 направлен от чертежа к читателю).
направлен от чертежа к читателю).
|
|
|




|
|
|



|
|


|
|
Рис. 1 Рис. 3
Произвольную площадь s можно изобразить вектором
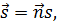
где 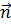 – положительная нормаль к площади s, направленная в сторону, с которой идущий по контуру площади s наблюдатель видит эту площадь слева от себя, т. е. в сторону, откуда обход по контуру кажется совершающимся против часовой стрелки.
– положительная нормаль к площади s, направленная в сторону, с которой идущий по контуру площади s наблюдатель видит эту площадь слева от себя, т. е. в сторону, откуда обход по контуру кажется совершающимся против часовой стрелки.
Вектор  может быть разложен на составляющие в декартовой прямоугольной системе координат
может быть разложен на составляющие в декартовой прямоугольной системе координат
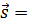 sx
sx 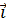 + sy
+ sy 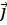 + sz
+ sz 
где sx, sy и sz – проекции площади s на координатные плоскости, т. е.
sx = s  , sy =
, sy =  sz = s
sz = s 
Теорема. Вектор замкнутого многогранника равен нулю.
Доказательство. Если s1,s2, …, sn – площади граней, составляющих часть поверхности некоторого многогранника, то вектор
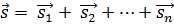
условимся называть вектором этой части поверхности s.
Чтобы убедиться, что для замкнутого многогранника  , достаточно показать, что в разложении
, достаточно показать, что в разложении
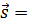 sx
sx 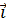 + sy
+ sy 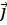 + sz
+ sz 
sx = 0, sy = 0 и sz = 0. Нетрудно сообразить, что проекция векторов всех граней замкнутого многогранника на любую плоскость равна нулю, так как при указанном выборе направления векторов отдельных граней все они будут либо внешними, либо внутренними.
Следовательно, алгебраическая сумма их проекций на какое-либо одно направление будет равна нулю.
По способу пределов понятие о векторе площади и доказанная теорема могут быть распространены на кривую замкнутую (регулярную) поверхность. При этом элемент поверхности ds представляется вектором 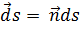 , где
, где 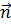 – вектор внешней нормали к замкнутой поверхности в данной её точке.
– вектор внешней нормали к замкнутой поверхности в данной её точке.
|
|
|
|
|
|
|
|
Дата добавления: 2014-11-28; Просмотров: 840; Нарушение авторских прав?; Мы поможем в написании вашей работы!