Уравнения движения приведенного механизма

Механизм даже с одной степенью свободы представляет собой сложную динамическую систему. Его звенья, имея определенные массы и моменты инерции, нагружаются при движении многочисленными силами и моментами сил. При выполнении динамического анализа такой механизм заменяется расчетной динамической моделью, состоящей из звена приведения. Энергетические параметры механизма и его расчетной динамической модели идентичны.

Пусть звено приведения совершает вращательное движение, обладает приведенным моментом инерции J_пр и на него действует приведенный момент сил М_пр. Параметры J_пр и М_пр являются функциями положения звена приведения, которое меняется со временем, т.е. φ = φ(t):

J_пр = J_пр (φ); М_пр = М_пр (φ). (3.53)

Для получения уравнения движения приведенного механизма используем уравнение Лагранжа 2-го рода (3.27). Обобщенной координатой в этом случае будет являться угол поворота звена q = φ, с обобщенной скоростью . Кинетическая энергия механизма равна

, (3.54)

где ω – угловая скорость звена приведения.

Уравнение Лагранжа 2-го рода запишем в виде

. (3.55)

Обобщенную силу определим из уравнения элементарной работы всех сил, приведенных к звену приведения,

δW = М_пр·δφ = Q_φ·δφ, (3.56)

где М_пр – приведенный момент сил; δφ – элементарный угол поворота звена приведения.

Тогда обобщенная сила Q_φ = М_пр.

Вычисляем производные от выражения кинетической энергии (3.54), учитывая зависимости (3.53):

;

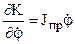. (3.57)

Подставив в уравнение (3.55) производные от выражения кинетической энергии (3.57) и обобщенную силу Q_φ, получим уравнение движения звена приведения, совершающего вращающее движение

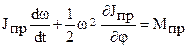. (3.58)

Рассмотрим расчетную динамическую модель механизма, состоящего из звена приведения, обладающего приведенной массой m_пр в точке приложения приведенной силы F_пр. Обобщенной координатой в этом случае будет являться перемещение точки: q = S.

Кинетическая энергия механизма определяется по формуле

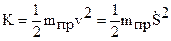, (3.59)

где v = – скорость точки приведения.

Уравнение Лагранжа 2-го рода запишем в виде

. (3.60)

Элементарная работа приведенных сил равна δW = F_прδS = Q_S·δS. Откуда выразим обобщенную силу Q_S = F_пр.

Взяв соответствующие производные кинетической энергии (3.59) и подставив их в уравнение (3.60), получим

. (3.61)

Дифференциальные уравнения (3.58) и (3.61) движения приведенных механизмов могут быть решены относительно скоростей или 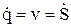. Далее определяют закон движения звена приведения:

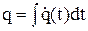. (3.62)

Зная эту функцию, по известным кинематическим функциям можно рассчитать параметры движения ведомых звеньев механизма.

Если приведенный момент инерции J_пр и приведенная масса m_пр – постоянные величины или близки к этому, то уравнения (3.58) и (3.61) примут вид

; (3.63)

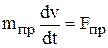. (3.64)

Дата добавления: 2014-11-29