Определение деформаций при изгибе

При изгибе деформация в поперечном сечении стержня (рис. 5.24, а) определяется перемещением у центра масс сечения в направлении, перпендикулярном первоначальному положению оси стержня, называемым прогибом и углом поворота θ сечения по отношению к своему первоначальному положению. Для нахождения деформаций во всех поперечных сечениях по длине стержня необходимо получить зависимости у = y(x) и θ = θ(x). Первую называют уравнением изогнутой оси или уравнением прогибов.

в

д

г

б

а

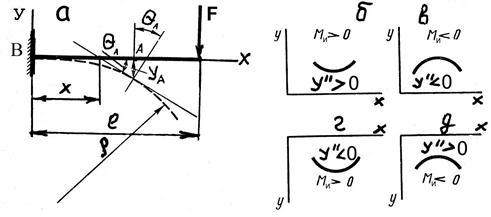
Рис. 5.24

Касательная к изогнутой оси стержня в любой ее точке составит с первоначальной осью угол, равный углу поворота θ сечения в данной точке. Тангенс угла θ наклона касательной tg θ = dy/dx. Но так как фактические значения углов поворота поперечных сечений при изгибе малы, порядка тысячных долей радиана, можно тангенс угла приравнять значению угла (tgθ ≈ θ) и найти связь между углом поворота сечения и прогибом в виде зависимости θ ≈ ≈ dy/dx.

Из курса математики известна следующая зависимость для кривизны K линии, расположенной в плоскости x0y:

. (5.76)

Но так как (dy/dx)² = tg²θ = θ² << 1, то выражение (5.76) упростим, представив в виде

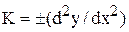. (5.77)

Используя зависимость (5.67), свяжем кривизну оси стержня с изгибающим моментом М_и и жесткостью поперечного сечения EI_z:

K = 1/ρ = М_и/(EI_z). (5.78)

Сравнивая полученные выражения кривизны в зависимостях (5.77) и (5.78), получим дифференциальное уравнение изогнутой оси стержня:

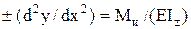, (5.79)

интегрирование которого не представляет затруднений. Выбор знака в выражении (5.79) определяется принятой системой координат. Принятый ранее знак изгибающего момента М_и (рис. 5.24, б, в, г, д) не зависит от направления координатных осей. Кривизна линии положительная, т.е. y'' = d²y/dx² > 0, если вогнутость кривой совпадает с положительным направлением оси у (рис. 5.24, б, д) и наоборот (рис. 5.24, в, г). При принятом направлении оси у вверх, знаки правой и левой частей уравнения (5.79) всегда одинаковы, т.е. при y'' > 0 и М_и > 0, а при y'' < 0 и М_и < 0. Поэтому выражение (5.79) представим как

d²y/dx² = М_и/ (EI_z). (5.80)

Для нахождения уравнений, определяющих деформации сечений стержня или их угловые и линейные перемещения, необходимо произвести интегрирование уравнения (5.80). Проинтегрировав уравнение (5.80) один раз, получим уравнение углов поворота

θ = dy/dx = . (5.81)

Интегрируя уравнение (5.80) второй раз, получим уравнение прогибов

, (5.82)

где С и D – постоянные интегрирования, определяемые из граничных условий, каковыми являются условия крепления изгибаемых стержней. Так, для стержня, жестко закрепленного одним концом, в месте крепления должны быть равны нулю и прогиб у, и угол поворота сечения. Для стержня, опирающегося на шарнирные крепления, прогиб равен нулю в местах крепления.

Пример. Определить прогиб и угол поворота свободного конца консоли стержня (рис. 5.24, а) длиной ℓ, нагруженного на конце сосредоточенной силой F. Жесткость стержня постоянна по длине и равна EI.

Начало координат примем в точке В жесткого закрепления стержня. Ось у направим вверх, ось х – вправо. В произвольном поперечном сечении, отстоящем на расстоянии х от начала координат, изгибающий момент равен М_и = –F (ℓ – x). Дифференциальное уравнение изогнутой оси (5.80) примет вид EI(d²y/dx²) = –F(ℓ – x). Интегрируя это уравнение, получим EI(dy/dx) = = –F × [ℓx – (x²/2)] + С. Интегрируя далее, получим уравнение прогибов

EIy = –F [(ℓx²/2) – (x³/6)] + Cx + D.

Приняв во внимание, что в месте закрепления при х =0 прогиб у и угол поворота сечения θ = dy/dx равны нулю, найдем, что постоянные интегрирования С =0 и D = 0. Тогда на свободном конце стержня при х = ℓ, прогиб
y = (–Fℓ³)/(3EI) и угол поворота торцового сечения θ = dy/dx = (–Fℓ²)/(2EI). Знак минус в выражениях прогиба и угла поворота указывает, что прогиб осуществляется в направлении, противоположном положительному направлению оси у, т.е. вниз, а торцовое сечение поворачивается по направлению движения часовой стрелки.

Дата добавления: 2014-11-29