Определение касательных напряжений при изгибе

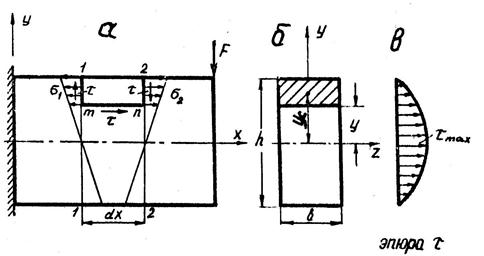
При поперечном изгибе в поперечном сечении помимо изгибающего момента действует поперечная сила Q. Рассмотрим жестко закрепленный одним концом стержень (рис. 5.23, а) прямоугольного сечения, нагруженный на свободном конце сосредоточенной силой F. Размеры сечения: высота h, ширина b. Двумя поперечными сечениями 1 – 1 и 2 – 2, отстоящими друг от друга на расстоянии d x, и горизонтальной плоскостью mn, расположенной на расстоянии у от нейтральной оси, выделим элементарный объем 1mn2. На этот элемент действуют следующие силы. По грани 1m действуют нормальные напряжения σ₁ = (М_и1·y)/I_z и пока неизвестные касательные напряжения τ, которые считаем равномерно распределенными по ширине b. По грани 2n действуют нормальные σ₂ = (М_и2·y)/ I_z и касательные напряжения τ, где М_и1 и М_и2 – изгибающие моменты в сечениях 1-1 и 2-2, а I_z – момент инерции поперечного сечения относительно нейтральной оси z. По грани mn действуют только касательные напряжения τ, равные, согласно закону парности, касательным напряжениям на вертикальных гранях. Равнодействующая нормальных к грани 1-1 составляющих внутренних сил 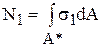, равнодействующая нормальных к грани 2-2 сил – 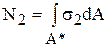, где А^* – площадь вертикальных граней выделенного объема в поперечных сечениях.

Уравнение равновесия сил, действующих на выделенный объем в виде проекций на продольную ось будет

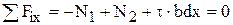, (5.73)

где τ·bdx – усилие, действующее по грани mn, связанное с касательными напряжениями. Из уравнения (5.73) можно выразить, что

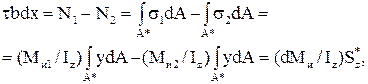(5.74)

где dМ_и = М_и1 – М_и2 – приращение изгибающего момента на длине стержня dx; 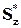– статический момент отсеченной части поперечного сечения относительно нейтральной оси; I_z – момент инерции поперечного сечения относительно нейтральной оси.

Из (5.74) выразим τ как τ = (dМ_и/dx)·(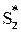 /I_zb). Учитывая зависимость (5.63), где производная dМ_и/dx равна поперечной силе Q, имеем формулу Д.И. Журавского для определения касательных напряжений

τ = (Q· 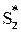)/I_zb. (5.75)

Распределение по сечению касательных напряжений для стержня любой формы определяется законом распределения статического момента 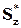, так как остальные величины выражения (5.75) для поперечного сечения постоянны.

б

а

в

Рис. 5.23

Рассмотрим изменение τ для стержня прямоугольного сечения (рис. 5.23, б). Статический момент заштрихованной площадки относительно нейтральной
оси z равен 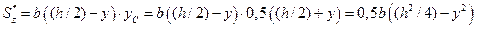, где 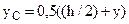– расстояние от оси z до центра масс отсеченной части сечения. Это уравнение параболы. Касательные напряжения определим по формуле (5.75), учитывая, что I_z = bh³/12;

.

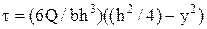Эпюру касательных напряжений (рис. 5.23, в) строим по трем точкам: τ_{y = h/2} = τ_{y = –h/2} = 0; τ_{y = 0} = 1,5 (Q/A).

Наибольшие касательные напряжения в поперечном сечении действуют на уровне нейтральной оси. Для стержней прямоугольного сечения они в 1,5 раза больше того напряжения, которое получилось бы при равномерном распределении касательных напряжений по сечению.

Касательные напряжения при изгибе максимальны на нейтральной оси и при других формах поперечного сечения. Для стержней круглого поперечного сечения они равны τ_max = (4/3)(Q/A), для стержней кольцевого сечения – τ_max = 2(Q/A).

Условие прочности стержней при изгибе по касательным напряжениям имеет вид τ_max ≤ τ_adm, где τ_adm – допускаемое напряжение материала стержня на срез или сдвиг. Отметим, что касательные напряжения в поперечных сечениях изгибаемых стрежней много меньше нормальных, поэтому расчет на прочность ведут обычно по нормальным напряжениям в соответствии с выражением (5.70) без учета влияния поперечных сил.

Дата добавления: 2014-11-29