Определение нормальных напряжений при изгибе

Рассмотрим прямолинейный стержень постоянного поперечного сечения прямоугольной формы площадью А (рис. 5.22, а), который изгибается (рис. 5.22, б) под действием двух внешних моментов М_е, приложенных в плоскости x0y к его концам. При таком нагружении в поперечных сечениях присутствуют только изгибающие моменты, т.е. стержень испытывает чистый изгиб. Если до деформации на боковую поверхность стержня (рис. 5.22, а) нанести координатную сетку, то при изгибе заметим следующее (рис. 5.22, б): линии сетки, параллельные оси стержня, изогнутся, сохранив между собой прежние расстояния, причем на выпуклой стороне (ab) удлинятся, что свидетельствует об их растяжении, а на вогнутой (ef) – станут короче; линии, перпендикулярные оси стержня (1 – 1; 2 – 2), останутся прямыми, но наклонятся относительно друг друга.

Считаем, что поперечные сечения, плоские до деформации, останутся плоскими и после деформации. При переходе от растянутой к сжатой части изгибаемого стержня имеется слой (сd), не испытывающий при изгибе ни сжатия, ни растяжения, называемый нейтральным слоем. Линия пересечения нейтрального слоя с плоскостью поперечного сечения стержня называется нейтральной осью. Как видно, волокна стержня деформируются различно. Выделим элемент стержня, ограниченный двумя поперечными сечениями, находящимися на бесконечно малом расстоянии dx друг от друга. При изгибе сечения АС и BD повернутся друг относительно друга на угол dθ. Волокно m-n, принадлежащее нейтральному слою (рис. 5.22, б), сохранит свою первоначальную длину dx, а волокно АВ, отстоящее на расстоянии y от нейтрального слоя, будет иметь длину dx'. Радиус кривизны дуги mn изогнутой оси стержня можно считать постоянным ρ. Относительная деформация волокна

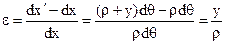(5.64)

прямо пропорциональна расстоянию y от него до нейтрального слоя, где ρ – радиус кривизны нейтрального слоя (изогнутой оси).

в

а

б

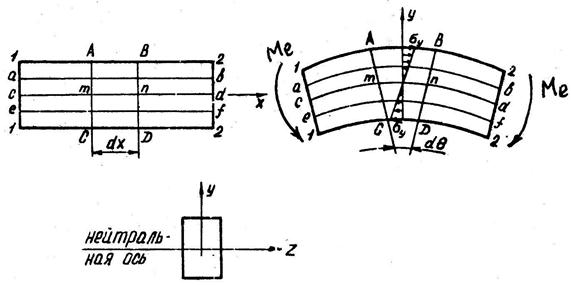
Рис. 5.22

При чистом изгибе касательные напряжения отсутствуют в поперечных сечениях стержня. Предполагается, что продольные волокна не давят друг на друга, они испытывают одноосное растяжение или сжатие. Зависимость, полученная на основании этого предположения, дает результаты, хорошо согласующиеся с данными экспериментов.

Согласно закону Гука для растяжения или сжатия, напряжение в слое, отстоящем на расстоянии у от нейтрального слоя, будет равно

σ_y = Eε = Ey/ρ. (5.65)

Из уравнения (5.65) видно, что нормальные напряжения отсутствуют в нейтральном слое и максимальны в волокнах, наиболее удаленных от нейтрального слоя. Но так как не известны ни ρ, ни положение нейтрального слоя, формула (5.65) не применяется в инженерных расчетах.

Свяжем действующие в точках сечения напряжения с внутренними силами поперечного сечения при чистом изгибе. Используя метод сечений, определим, что не только поперечные Q, но и продольная N силы отсутствуют, т.е. N = F_ix = 0. Элементарная продольная сила в сечении, действующая на площадку dA, равна dN = σ_ydA, а сумма таких сил по сечению – 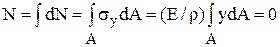. Но E/ρ ≠ 0, так как рассматривается изогнутый стержень, радиус кривизны оси которого ρ ≠ ∞, следовательно, 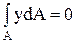. Данный интеграл равен статическому моменту поперечного сечения относительно нейтральной оси (рис. 5.22, в). Так как он равен нулю, нейтральная ось (z) проходит через центр масс сечения (п. 5.11.1). Координата у в выражении (5.65) получает определенность, она равна расстоянию до оси, проходящей через центр масс поперечного сечения.

Изгибающий момент в сечении М_и= 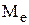. При заданной плоскости действия момента М_е внешних сил, изгибающий момент равен моменту внутренних сил в этой же плоскости, т.е. относительно нейтральной оси. Выразим изгибающий момент через элементарные внутренние силы dN. При принятом направлении осей М_иу = 0, а полный изгибающий момент

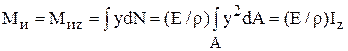, (5.66)

где 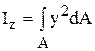– момент инерции сечения относительно нейтральной оси; ρ – радиус кривизны изогнутого нейтрального слоя. Выразим из (5.66) кривизну нейтрального слоя:

1/ρ = М_и/(EI_z). (5.67)

Подставив значение 1/ρ в выражение (5.65), получим зависимость

σ_y = (M_и·y)/I_z, (5.68)

позволяющую определить нормальные напряжения в любой точке сечения стержня по известным изгибающему моменту М_и и моменту инерции сечения I_z относительно оси, проходящей через центр масс сечения.

Из выражения (5.68) видно, что нормальные напряжения для нейтрального слоя, когда у = 0, равны нулю, а максимальные нормальные напряжения будут в наиболее удаленных от нейтрального слоя волокнах (рис. 5.22, б), когда у = у_max. При расчетах на прочность представляют интерес прежде всего наибольшие по величине напряжения, в поперечном сечении они равны

σ = (М_и·y_max)/I_z = М_и/W_z, (5.69)

где W_z = I_z/y_max – осевой момент сопротивления сечения или момент сопротивления при изгибе. Он является геометрической характеристикой поперечного сечения стержня, влияющей на его прочность при изгибе. Момент сопротивления для стержней с прямоугольным сечением (см. рис. 5.16, а) со сторонами h и b равен W_z = bh²/6, а для стержней с круглым поперечным сечением (рис. 5.16, б) диаметром d – W_z ≈ 0,1 d³.

Установлено, что формулы (5.68), (5.69) несмотря на то, что выведены для чистого изгиба, применимы и дают надежные результаты при поперечном изгибе.

Условие прочности стержня постоянного поперечного сечения (W_z = const) при изгибе по нормальным напряжениям имеет вид

σ_max = М_иmax/W_z ≤ σ_adm, (5.70)

где σ_adm – допускаемое напряжение материала на растяжение; М_иmax – максимальный изгибающий момент в поперечном сечении по длине стержня, находится из эпюры изгибающего момента М_и =М_и(х). При выборе сечения изгибаемого стержня используют зависимость

W_z ≥ М_иmax/ σ_adm. (5.71)

Размеры прямоугольного или круглого поперечного сечения определяют по приведенным выше зависимостям; для сечений металлопроката (двутавры, швеллеры, уголки и т.п.) значения W_z указаны в таблицах сортамента.

Предельный изгибающий момент определяется как

М_иu ≤ W_z·σ_adm. (5.72)

Зная связь между М_иu и нагрузкой при построении эпюры изгибающего момента находят предельную или допускаемую нагрузку.

Стержни, выдерживающие одинаковый предельный изгибающий момент, имеют одинаковый момент сопротивления сечения W_z. Чем меньше при этом площадь А поперечного сечения стержня, тем рациональнее с точки зрения затрат материала конструкция. Для оценки рациональности сечений может служить безразмерная величина W_z / 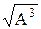. Для круга и квадрата она равна соответственно 0,14 и 0,167; для швеллера – 0,57 … 1,35; для двутавра – 1,02 …1,51. Наиболее рационально использовать в конструкциях, работающих на изгиб двутавры, швеллера.

Дата добавления: 2014-11-29