Определение деформаций при кручении стержней с круглым поперечным сечением

Деформация при кручении стержней определяется углом поворота поперечных сечений относительно начального положения. Воспользуемся формулой (5.49) для выражения угла поворота сечения скручиваемого стержня на участке длиной dx

dφ = (Tdx)/GI_p. (5.55)

Полный угол закручивания на участке длиной ℓ равен

. (5.56)

Если крутящий момент T и величина GI_p, называемая жесткостью при кручении, постоянны на всей длине ℓ, то полный угол закручивания в радианах будет равен

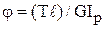. (5.57)

Расчет стержней на прочность при кручении не исключает возможности возникновения недопустимых деформаций (углов поворота поперечных сечений) при целостности длинных стержней (деталей). Поэтому часто детали, испытывающие деформацию кручения, рассчитывают не только на прочность, но и на жесткость. Для обеспечения требуемой жесткости необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого, т.е.

(dφ/dx) = ≤ (dφ/dx)_adm, (5.58)

где (dφ/dx)_adm – допускаемый относительный угол закручивания в радианах на единицу длины стержня. Чаще (dφ/dx)'_adm задают в градусах на метр длины, тогда выражение (5.58) будет иметь вид

(dφ/dx)'_adm. (5.59)

Величину (dφ/dx)'_adm выбирают в зависимости от назначения детали и ее размеров. В приборостроении (dφ/dx)'_adm принимают в пределах 20 угловых минут на длине 1 м, т.е. (dφ/dx)'_adm. =0,33 |º/м|. Из условия жесткости (5.59) можно определить минимальный диаметр деформируемого стержня, учитывая, что I_p ≈ 0,1d⁴

(5.60)

или предельный по величине крутящий момент

T_u ≤19 GI_p. (5.61)

При совместных расчетах на прочность и жесткость при кручении диаметр стержня принимают равным наибольшему из найденных по формулам (5.54) и (5.60), а предельный крутящий момент Т_u ограничивают наименьшим, полученным при проверке по зависимостям (5.53) и (5.61).

Дата добавления: 2014-11-29