Частотное регулирование угловой скорости синхронных двигателей

Законы регулирования. Использование полупроводниковых пре-образователей частоты открывает большие возможности при создании электромеханических систем с СД. Эти системы обладают такими не-сомненными достоинствами, как стабильность угловой скорости незави-симо от момента нагрузки во всем диапазоне регулирования угловой скорости, большими значениями моментов на ползучих скоростях при регулировании напряжения и тока возбуждения. Они позволяют получить высокую точность синхронного движения управляемых машин.

Напомним, что электромагнитный момент СД с явно выраженными полюсами определяется следующей зависимостью:

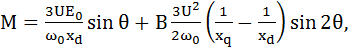(10.1)

где U – напряжение якоря; Е₀ – ЭДС, индуцируемая в обмотке якоря; w₀ – угловая скорость магнитного поля; x_d – синхронное индуктивное сопротивление по продольной оси; x_q – синхронное индуктивное соп-ротивление по поперечной оси; θ – угол нагрузки.

Это выражение удобно представить, пренебрегая насыщением, в виде

, (10.2)

где I_в – ток возбуждения СД; А и В – постоянные величины.

Рассмотрим режим работы СД при f = const; U = var; I _в = var. Этот режим является наиболее характерным для нерегулируемых систем с СД. Формула электромагнитного момента для этого случая имеет вид

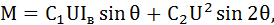(10.3)

где

.

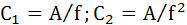Для характеристики электромеханических свойств удобно рассмат-ривать регулирование синхронного двигателя отдельно при I_В = var; U = const и I_В = const; U = var. Моментно-угловые характеристики при этом соответственно представлены на рис. 10.5 (при I_В = var; U = const:1 – нормальное возбуждение; 2 – повышенное возбуждение; 3 – пониженное возбуждение; М₁ – момент от явнополюсности; М – суммарный момент поля возбуждения) и 10.6 (при I_D = const; U = var: 1 – U = U_H0H;2 – U > tI_HOM; 3 – U << U_H0M; At,М₁ – момент от поля возбуждения; М₂ – момент от явнополюсности; М – суммарный момент).

При частотном регулировании СД, когда U 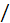f = const; I_В = var аналитическая зависимость для момента имеет вид

, (10.4)

где

.

Характеристики для этого случая представлены на рис.10.7.

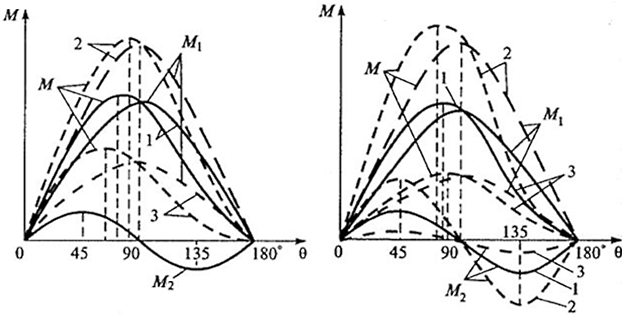
Рис. 10.5. Моментно-угловые характеристики СД

Рассмотрим режим частотного регулирования СД при U = const; I_В= = const; f = var. Формула электромагнитного момента:

где

C₁ = AUI_В;C₂ = BU² .

Из последнего выражения видно, что при сниженных угловых скоростях (частотах напряжения статора) СД обладает значительным максимальным моментом.

Закон регулирования напряжения и тока возбуждения неявнополюс-ного СД или приближенный закон регулирования для крупных явнопо-люсных СД при изменении угловой скорости (частоты) и момента наг-рузки и заданном запасе статической устойчивости найдем, воспользо-вавшись первой составляющей (10.2) для электромагнитного момента.

При постоянстве угла нагрузки СД закон регулирования напряжения и тока возбуждения находим следующим образом:

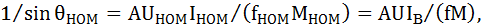
откуда

. (10.6)

При U/f = U_H0M 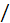f_HOM = const получим зависимость регулирования тока возбуждения СД от момента на валу:

. (10.7)

Из выражения (10.7) следует, что при постоянном отношении U 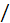f возбуждение СД должно изменяться прямо пропорционально изменению момента на валу.

Для I_В = I_{В НОМ} = const из (10.6) следует, что U 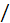f = U_HOM 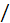f_HOM = const, и регулирование производится при постоянном моменте.U 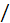f = const; I_В = var: 1 – нормальное возбуждение; 2 – повышенное возбуждение; 3 –по-ниженное возбуждение; М – момент от поля возбуждения; М₂ – момент от явнополюсности; М – суммарный момент.

Для СД с явно выраженными полюсами при существенном влиянии реактивной составляющей момента закон регулирования напряжения определяется таким же образом, как и для неявнополюсной машины. Из уравнения (10.1) при условии постоянства угла θ и тока возбуждения (I_В = const), приняв в ограниченном диапазоне регулирования угловой скорости E = U, получим

,

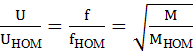т.е. закон регулирования имеет тот же вид, что и для АД при частотном управлении. Следовательно, и частотные законы регулирования для различного вида нагрузок будут одинаковыми для обоих типов машин:U/f = const приМ = М_НОМ = const, U/f = const приР = Р_НОМ = const; U/f² = const при вентиляторной нагрузке.

Частотное регулирование, являясь практически единственным спо-собом регулирования угловой скорости СД, характеризуется в основном такими же показателями, что и ^:частотное регулирование АД с КЗ ротором.

Дата добавления: 2014-11-29