
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Разработал: О.М. Аюбова 1 страница
|
|
|
|
Учебная дисциплина: Информатика
Специальности: 151001, 160203
Содержание
| Стр. | |
| 1 Самостоятельная работа № 1 «Числовая окружность. Синус, косинус, тангенс и котангенс числового аргумента». | |
| 2 Справочник. Решение типовых задач. Частных модулей 3.1, 3.2 | |
| 3 Самостоятельная работа № 2. Тестовая работа. «Основные тригонометрические тождества. Радианное и градусное измерение углов и дуг. Формулы приведения». | |
4 Самостоятельная работа № 3, 4. «Функции  , их графики и свойства». , их графики и свойства».
| |
| 5 Самостоятельная работа № 5 Расчётно – графическая работа «Графики тригонометрических функций. Преобразования графиков функций. Решение уравнений графическим методом». | |
| 6 Алгоритм решения простейших тригонометрических уравнений графическим методом. | |
| 7 Преобразование графиков функций | |
| 8 Решение типовых задач частного модуля 3.5 | |
| 9 Вопросы для самоконтроля расчётных модулей 3.1 – 3.5 | |
| 10 Самостоятельная работа № 6. Типовой расчёт «Основные формулы тригонометрии и следствия из них». | |
| 11 Краткий справочник основных формул тригонометрии. | |
| 12 Решение типовых задач частного модуля 3.6 | |
| 13 Самостоятельная работа № 7. Тестовая работа. «Решение простейших тригонометрических уравнений, неравенств». | |
| 14 Краткий справочник формул решения уравнений частного модуля 3.7 | |
| 15 Решение типовых задач частного модуля 3.7 | |
| 16 Алгоритм решения простейших тригонометрических уравнений. | |
| 17 Алгоритм решения простейших тригонометрических неравенств. | |
| 18 Самостоятельная работа № 8 «Решение тригонометрических уравнений». | |
| 19 Краткий справочник по решению тригонометрических уравнений с решением типовых задач частного модуля 3.8 | |
| 20 Инструкция к решению тригонометрических уравнений | |
| 21 Вопросы для самоконтроля частных модулей 3.7, 3.8 |
Модуль № 3 «Тригонометрические функции, их свойства и графики»
Целью данного пособия является формирование представления о тригонометрических функциях, их свойствах, графиках, формирование умений решать тригонометрические уравнения и неравенства, выполнять несложные тригонометрические преобразования.
Пособие содержит справочный материал, типовые задачи с подробным решением, самостоятельные работы и вопросы для самоконтроля.
Пособие отвечает требованиям обязательного минимума содержания образования по данной теме.
Самостоятельная работа студента (СРС)
СРС № 1 «Числовая окружность. Синус, косинус, тангенс и котангенс числового аргумента».
Форма организации: индивидуальная.
1 Цели работы: проверить сформированность умений работать с числовой окружностью, усвоение понятий синуса, косинуса, тангенса и котангенса числового аргумента, умение находить  .
.
2 Уровни усвоения:
Знать:
- понятие числовой окружности;
- определение единичной окружности;
- формулу длины окружности;
- определение 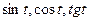 и
и  в тригонометрии;
в тригонометрии;
- знаки  в каждой из четвертей единичной окружности;
в каждой из четвертей единичной окружности;
- свойства: чётность, нечётность, периодичность синуса, косинуса, тангенса, котангенса числового аргумента;
- табличные значения  .
.
Уметь
- находить на числовой окружности точки, соответствующие заданному числу;
- определять взаимное расположение на числовой окружности точек, соответствующих данным числам;
- определять какой четверти числовой окружности принадлежит точка, соответствующая числу;
- находить декартовы координаты точек числовой окружности;
- вычислять значение синуса и косинуса.
3 Методические рекомендации и указания.
3.1 Работа состоит из 24 вариантов. Каждый вариант содержит по 5 типовых заданий:
- задания 1 – 3 направлены на формирование умений работать с числовой окружностью;
- задание 4 – на закрепление умений находить  с помощью числовой окружности;
с помощью числовой окружности;
- задание 5 – на закрепление свойств чётности, нечётности, периодичности синуса, косинуса, тангенса, котангенса числового аргумента и знаний табличных значений 
3.2 При выполнении работы студент может использовать:
- решение типовых задач учебно – методического пособия по данной теме;
- краткий справочник пособия;
- литературу:
- А. Г. Мордкович «Алгебра и начала анализа», ч.1 Учебник 10 – 11 классы. x 1 – 5;
- под редакцией Г.Н. Яковлева «Алгебра и начала анализа» математика для техникумов. Ч.1, стр.262, 263 (Наука М.1977).
4 Содержание работы:
Задание 1
Найдите на числовой окружности точки, соответствующие заданным числам.
1.1 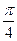 и
и 
1.2  и
и 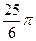
1.3  и
и 
1.4 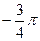 и
и 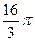
1.5  и
и 
1.6  и
и 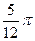
1.7  и
и 
1.8 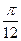 и
и 
1.9  и
и 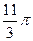
1.10 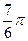 и
и 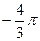
1.11 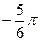 и
и 
1.12  и
и 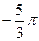
1.13 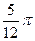 и
и 
1.14 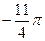 и
и 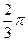
1.15 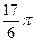 и
и 
1.16  и
и 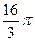
1.17  и
и 
1.18  и
и 
1.19  и
и 
1.20 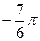 и
и 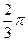
1.21  и
и 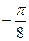
1.22  и
и 
1.23 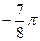 и
и 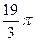
1.24 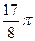 и
и 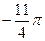
Задание 2
Определите, как расположены на числовой окружности точки, соответствующие числам:
2.1  и
и 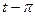
2.2  и
и 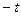
2.3  и
и 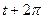
2.4  и
и 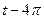
2.5 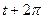 и
и 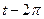
2.6  и
и 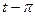
2.7  и
и 
2.8  и
и 
2.9  и
и 
2.10 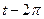 и
и 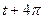
2.11  и
и 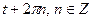
2.12  и
и 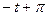
2.13  и
и 
2.14  и
и 
2.15  и
и 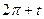
2.16 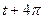 и
и 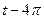
2.17  и
и 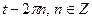
2.18 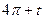 и
и 
2.19  и
и 
2.20  и
и 
2.21  и
и 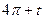
2.22  и
и 
2.23  и
и 
2.24  и
и 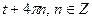
Задание 3
Найдите на числовой окружности точки с данной ординатой или абсциссой и запишите, каким числам они соответствуют.
3.1 
3.2 
3.3 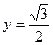
3.4 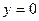
3.5 
3.6 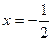
3.7 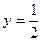
3.8 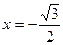
3.9 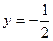
3.10 
3.11 
3.12 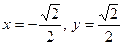
3.13 
3.14 
3.15 
3.16 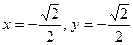
3.17 
3.18 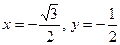
3.19 
3.20 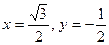
3.21 
3.22 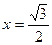
3.23 
3.24 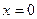
Задание 4
Найдите  , если:
, если:
4.1 
4.2 
4.3 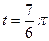
4.4 
4.5 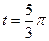
4.6 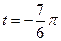
4.7 
4.8 
4.9 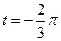
4.10 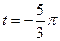
4.11 
4.12 
4.13 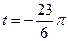
4.14 
4.15 
4.16 
4.17 
4.18 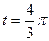
4.19 
4.20 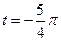
4.21 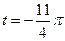
4.22 
4.23 
4.24 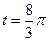
Задание 5
Вычислите:
5.1 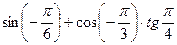
5.2 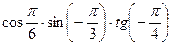
5.3 
5.4 
5.5 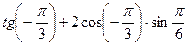
5.6 
5.7 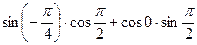
5.8 
5.9 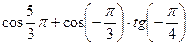
5.10 
5.11 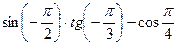
5.12 
5.13 
5.14 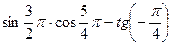
5.15 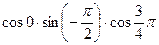
5.16 
5.17 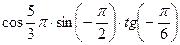
5.18 
5.19 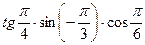
5.20 
5.21 
5.22 
5.23 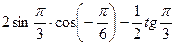
5.24 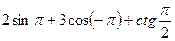
Справочник
1 Единичная окружность – модель для введения понятий тригонометрии.
Единичная окружность – окружность, радиуса 1 единица (Рис.1).
Длина окружности  .
.

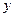
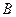
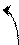


Рис. 1
 - горизонтальный диаметр единичной окружности,
- горизонтальный диаметр единичной окружности,
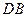 - вертикальный диаметр окружности.
- вертикальный диаметр окружности.
Точка  - начальная (стартовая) точка.
- начальная (стартовая) точка.
Пусть дана единичная окружность и на ней отмечена начальная точка 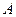 . Поставим в соответствие каждому действительному числу
. Поставим в соответствие каждому действительному числу  точку окружности по следующему правилу:
точку окружности по следующему правилу:
1) Если  , то двигаясь из точки
, то двигаясь из точки 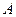 в направлении против часовой стрелки (положительное направление обхода окружности) опишем по окружности путь
в направлении против часовой стрелки (положительное направление обхода окружности) опишем по окружности путь 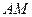 длиной
длиной  . Точка
. Точка  и будет искомой точкой
и будет искомой точкой 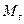 .
.
2) Если  , то двигаясь из точки
, то двигаясь из точки 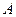 в направлении по часовой стрелки (отрицательное направление обхода окружности) опишем по окружности путь
в направлении по часовой стрелки (отрицательное направление обхода окружности) опишем по окружности путь 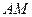 длиной
длиной 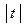 . Точка
. Точка  и будет искомой точкой
и будет искомой точкой 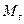 .
.
3) Числу 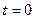 поставим в соответствие точку
поставим в соответствие точку 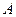 .
.
Единичную окружность с установленным соответствием (между действительными числами и точками окружности) называют числовой окруджностью.
È  - называют I четвертью единичной окружности. - называют I четвертью единичной окружности.
| È 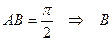 соответствует соответствует 
|
È 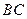 - II четвертью. - II четвертью.
| È  соответствует соответствует 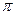
|
È 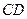 - III четвертью. - III четвертью.
| È 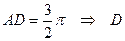 соответствует соответствует 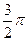
|
È  - IV четвертью. - IV четвертью.
| 
|
Ясно, что  соответствует число
соответствует число  ,
, 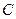 соответствует число
соответствует число 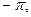
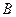 соответствует число
соответствует число  ,
, 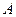 соответствует число
соответствует число  , где
, где  и т.д.
и т.д.

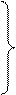
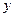


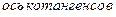
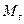

 | |||
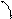 | |||
|
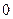



 - ордината точки
- ордината точки 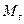 единичной окружности;
единичной окружности;
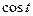 - абсцисса точки
- абсцисса точки 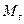 единичной окружности;
единичной окружности;
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 593; Нарушение авторских прав?; Мы поможем в написании вашей работы!