КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Разработал: О.М. Аюбова 5 страница
|
|
|
|
4.22  и
и 
А  и и 
| Б  и и 
| В  и и 
| Г  и и 
| Д 
|
4.23 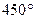 и
и 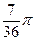
А  и и 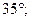
| Б 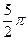 и и 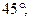
| В 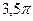 и и 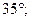
| Г  и и 
| Д 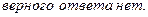
|
4.24  и
и 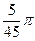
А  и и 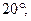
| Б  и и 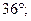
| В  и и 
| Г  и и 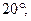
| Д 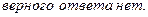
|
СРС № 3, 4
«Функции  ,
,  , их графики и свойства»
, их графики и свойства»
Форма организации: индивидуальная.
1 Цели работы: построить графики функций  ,
,  и по графикам выполнить исследование функций по схеме исследования функций.
и по графикам выполнить исследование функций по схеме исследования функций.
2 Уровни усвоения.
Знать:
- схему исследования функций;
- вид графиков функций  ,
, 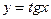 ;
;
- свойства функций  ,
, 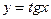 ;
;
- простейшие преобразования графиков функций;
- формулы приведения.
Уметь:
- используя формулы приведения, выразить  через
через  ;
;
- выполнив простейшие преобразования, построить графики  ,
,  ;
;
- по графикам функций  ,
,  прочитать свойства функций и записать их согласно схеме исследования функций.
прочитать свойства функций и записать их согласно схеме исследования функций.
3 Методические рекомендации и указания.
3.1 Работа выполняется в два этапа после изучения тем «Функция  , её график и свойства», «Функция
, её график и свойства», «Функция 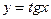 , её график и свойства» соответственно.
, её график и свойства» соответственно.
3.2 Рабочие конспекты составляются по плану:
1 Записывается тема.
2 По формулам приведения косинус (котангенс) выражается через синус (тангенс).
3 Строится график изучаемой функции.
4 По графику читаются свойства функции и записываются согласно схеме исследования функции.
3.3 После составления рабочего конспекта выполняется самопроверка по образцу и вопросам для самоконтроля.
3.4 При выполнении работы студент может использовать:
- схему исследования функции;
- литературу:
- А.Г. Мордкович «Алгебра и начала анализа», часть 1, учебник 10 – 11 кл. x 9, 10, 11, 15;
- «Алгебра и начала анализа». Часть 1 (учебник для техникумов) под редакцией Г.Н. Яковлева, глава V x 29.
СРС № 5
Расчётно – графическая работа
«Графики тригонометрических функций. Преобразования графиков функций.
Решение уравнений графическим методом»
Форма организации: работа в парах.
1 Цели работы: закрепить и углубить знания о преобразованиях графиков функций, умения строить графики тригонометрических функций, переходить от одного способа задания к другому и решать тригонометрические уравнения графическим методом.
2 Уровни усвоения.
Знать:
- графики элементарных функций;
- способы задания функций;
- виды преобразований графиков функций;
- графики функций  ;
;
- алгоритм решения тригонометрических уравнений графическим методом.
Уметь:
- строить графики элементарных функций (в том числе и графики  );
);
- выполнять преобразования графиков тригонометрических функций и описывать эти преобразования;
- по аналитическому заданию функции описывать построение графика функции;
- по графику функции задавать функцию аналитически;
- решать несложные тригонометрические уравнения графическим методом.
3 Методические рекомендации и указания.
3.1 Работа состоит из 15 вариантов (3 последних повышенной сложности, отмечены *). Каждый вариант содержит 3 задания:
· задание 1 – решение уравнений вида 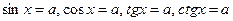 и сводящихся к ним;
и сводящихся к ним;
· задание 2 – описание выполняемых преобразований с графиком тригонометрической функции и построение графика данной функции;
· задание 3 – исследование графика функции и задание данной функции аналитическим способом.
3.2 При выполнении работы студент может использовать:
- алгоритм решения простейших тригонометрических уравнений графическим методом;
- краткий справочник «Преобразование графиков функций»;
- литературу:
- А.Г. Мордкович «Алгебра и начала анализа», часть 1, учебник 10 – 11 кл. Глава I, x 9 - x13, x18;
- «Алгебра и начала анализа». Часть 1 (учебник для техникумов) под редакцией Г.Н. Яковлева, глава V, x 35.
3.3 Студентам предлагается для дополнительной работы выполнить задания повышенной сложности (варианты 13 - 15). Для получения «удовлетворительно» достаточно выполнить задание 1а и задание 2а или 3, на «хорошо» задание 1а, 2а и 3, на «отлично» задание 1а,б; 2 а, б и 3.
4 Содержание работы.
Задание 1. Решите уравнения графически:
1.1 а) 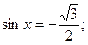 б)
б) 
1.2 а)  б)
б) 
1.3 а)  б)
б) 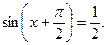
1.4 а) 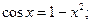 б)
б) 
1.5 а)  б)
б) 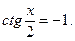
1.6 а)  б)
б) 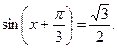
1.7 а)  б)
б) 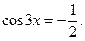
1.8 а)  б)
б) 
1.9 а)  б)
б) 
1.10 а)  б)
б) 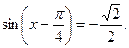
1.11 а) 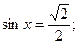 б)
б) 
1.12 а)  б)
б) 
1.13* а)  б)
б) 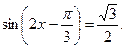
1.14* а)  б)
б) 
1.15* а)  б)
б) 
Задание 2. 2.1 Опишите построение графика функции по её аналитическому заданию.
2.2 Постройте график функции.
2.1 
2.2 
2.3 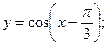
2.4 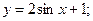
2.5 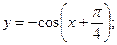
2.6 
2.7 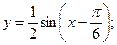
2.8 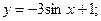
2.9 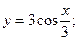
2.10 
2.11 
2.12 
2.13* 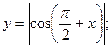
2.14* 
2.15* 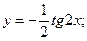
Задание 3. Задайте аналитически функцию, график которой изображён.
3.1
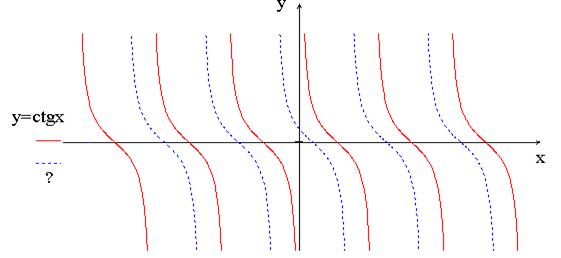
3.2

3.3

3.4

3.5
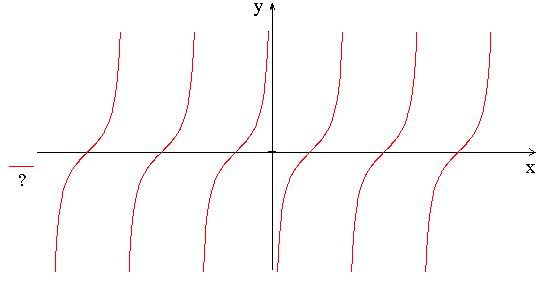
3.6
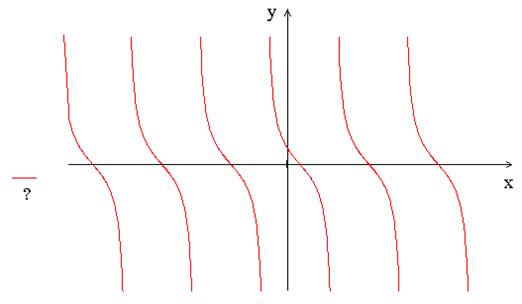
3.7

3.8
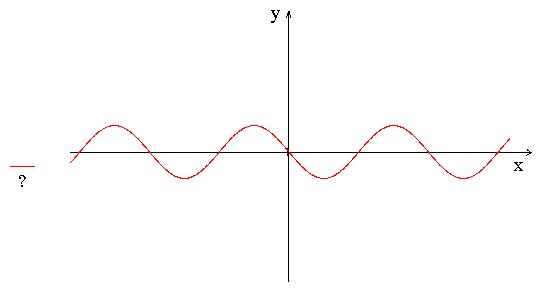
3.9

3.10

3.11

3.12

3.13

3.14

3.15

Алгоритм решения простейших
тригонометрических уравнений графическим методом
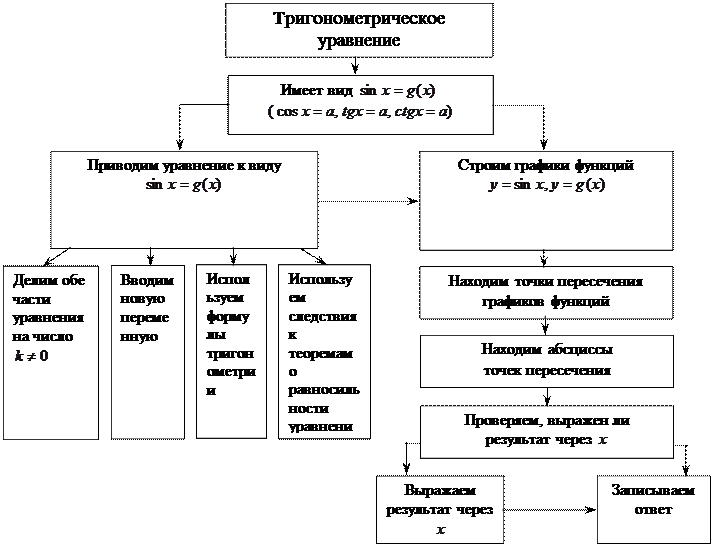
Нет Да
Нет Да
Решение задач
Задача 1. Решить графически уравнение: 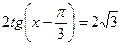 .
.
Решение:

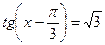 - строим
- строим 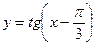 и
и  в одной системе координат и находим абсциссы точек пересечения или: пусть
в одной системе координат и находим абсциссы точек пересечения или: пусть  , тогда получим уравнение
, тогда получим уравнение 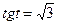 .
.
Строим в одной и той же системе координат графики 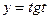 и
и  .
.
      
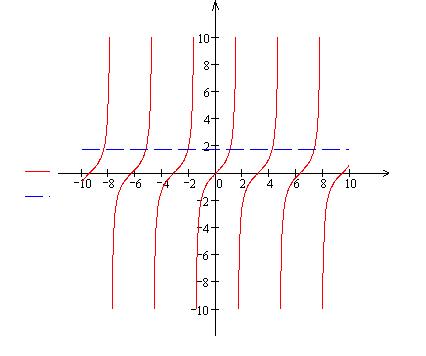
| По графику находим, что   или или  , ,  , тогда , тогда  , ,  , т.е. , т.е. 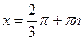 , ,  Ответ:
Ответ: 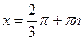 , , 
|
Задача 2. Описать построение графика: а) 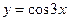 ; б)
; б) 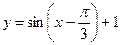 и построить его.
и построить его.
Решение:
а) Построим полуволну графика  и выполним её сжатие к оси
и выполним её сжатие к оси  с коэффициентом 3, затем построим весь график.
с коэффициентом 3, затем построим весь график.
|
|
|


|
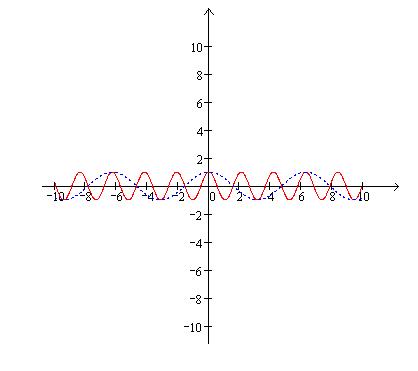
б) Построим синусоиду (полуволну графика  ), выполним её сдвиг на
), выполним её сдвиг на  ед. вправо, а затем сдвиг на 1 ед. вверх вдоль оси
ед. вправо, а затем сдвиг на 1 ед. вверх вдоль оси 
|

|

|
|
|
|

Или: Построим новую систему координат 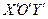 , где
, где 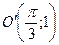 и в ней график
и в ней график 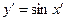 - это и будет график
- это и будет график  в «старой» системе координат.
в «старой» системе координат.
Преобразование графиков функций
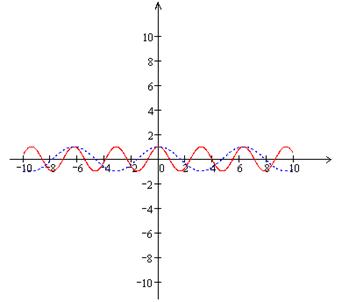
1 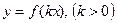 - график этой функции получается из графика
- график этой функции получается из графика 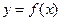
· сжатием к оси ординат ( ), если
), если 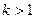 ;
;
· растяжением от оси  , если
, если  .
.
|

|
2 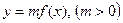 - график этой функции получается из графика
- график этой функции получается из графика 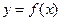
· растяжение от оси абсцисс (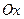 ), если
), если  ;
;
· сжатием к оси 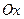 , если
, если 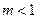 .
.

|

|
3 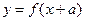 - график этой функции получается из графика
- график этой функции получается из графика 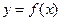 параллельным переносом вдоль оси
параллельным переносом вдоль оси 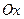 на
на  единиц:
единиц:
· влево, если  ;
;
· вправо, если  .
.
4  - график этой функции получается из графика
- график этой функции получается из графика 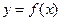 параллельным переносом вдоль оси
параллельным переносом вдоль оси  на
на  единиц:
единиц:
· вверх, если  ;
;
· вниз, если  .
.
5  - график этой функции получается из графика
- график этой функции получается из графика 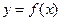 , путём преобразования симметрии относительно оси
, путём преобразования симметрии относительно оси 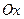 .
.

|

|
|
|

|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 325; Нарушение авторских прав?; Мы поможем в написании вашей работы!