Разработал: О.М. Аюбова 6 страница

Вопросы для самоконтроля

1 Какую окружность называют единичной, числовой?

2 Зачем вводится новая математическая «единичная окружность»?

3 Что такое синус, косинус, тангенс, котангенс числового аргумента?

4 Где и как отмечают значения ?

5 Какие знаки имеют в каждой числовой четверти?

6 В какой четверти единичной окружности:

· имеют одинаковый знак;

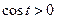· и ;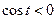

· и ;

· и .

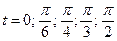7 Каковы значения для и ?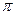

8 Что вы можете рассказать о градусной и радианной мерах углов и дуг? Каковы соотношения между этими мерами?

9 Что такое 1 радиан?

10 Какова градусная мера 1 радиана?

11 Какими свойствами обладают и ?

12 Формулы, какого вида называют формулами приведения?

13 Для чего нужны формулы привидения?

14 Каковы правила запоминания формул приведения?

15 Назовите основные тригонометрические тождества. Как их получить?

16 Назовите тригонометрические функции числового аргумента. Какое название имеет график каждой из этих функций?

17 Каков период, основной период каждой тригонометрической функции? ?

18 Какими свойствами обладают тригонометрические функции?

19 Какие преобразования выполнимы с графиками тригонометрических функций? В чём суть этих преобразований?

СРС № 6

Типовой расчёт

«Основные формулы тригонометрии и следствия из них»

Форма организации: индивидуальная.

1 Цели работы: закрепить и углубить умения вычислять значения тригонометрических функций, используя основные формулы тригонометрии и следствия из них.

2 Уровни усвоения.

Знать:

- основные соотношения между тригонометрическими функциями одного аргумента;

- формулы синуса, косинуса, тангенса суммы и разности двух аргументов;

- формулы синуса, косинуса, тангенса двойного и половинного аргументов;

- формулы преобразования произведения тригонометрических функций в сумму и разность;

- формулы преобразования суммы (разности) синусов, косинусов в произведение.

Уметь:

- выражать тригонометрические функции через значение одной из них;

- находить значения тригонометрических функций, используя основные формулы тригонометрии и следствия из них.

3 Методические рекомендации и указания.

3.1 Работа состоит из 24 вариантов. Каждый вариант содержит 5 заданий, которые дают возможность закрепить и углубить знания основных формул тригонометрии и умения использовать их при вычислении значений тригонометрических функций.

· задание 1 – использование формул синуса, косинуса, тангенса суммы, разности двух аргументов;

· задание 2 – использование формул двойного аргумента;

· задание 3 – использование формул половинного аргумента, двойного аргумента;

· задание 4 – использование формул преобразования произведения тригонометрических функций в сумму, разность и суммы; разности синусов, косинусов в произведение;

· задание 5 – использование различных формул тригонометрии, которые студент выбирает самостоятельно. Предназначено для дополнительной работы.

3.2 При выполнении типового расчёта студент может использовать:

- краткий справочник формул;

- примеры решения задач с применением основных формул;

- литературу «Алгебра и начала анализа». Часть 1 (учебник для техникумов) под редакцией Г.Н. Яковлева, глава V x 31.

4 Содержание работы.

Задание 1. Вычислите:

1.1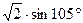

1.2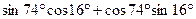

1.3

1.4

1.5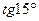

1.6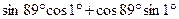

1.7 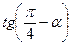, если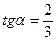

1.8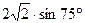

1.9

1.10

1.11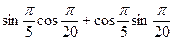

1.12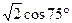

1.13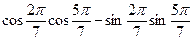

1.14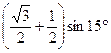

1.15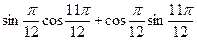

1.16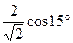

1.17 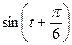, если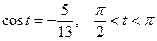

1.18 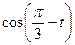, если

1.19 , если

1.20 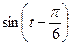, если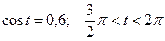

1.21 , если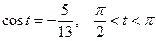

1.22 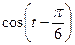, если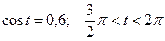

1.23 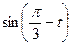, если

1.24

Задание 2. Найдите:

2.1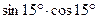

2.2

2.3

2.4

2.5

2.6

2.7

2.8

2.9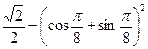

2.10

2.11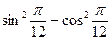

2.12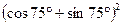

2.13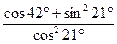

2.14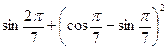

2.15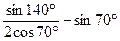

2.16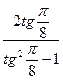

2.17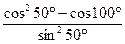

2.18

2.19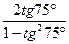

2.20

2.21

2.22

2.23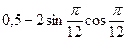

2.24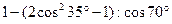

Задание 3. Найдите:

3.1 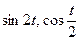, если

3.2 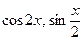, если

3.3 , если

3.4 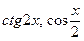, если

3.5 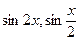, если

3.6 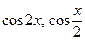, если

3.7 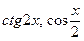, если

3.8 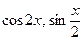, если

3.9 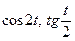, если

3.10 , если

3.11 , если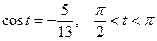

3.12 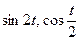, если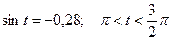

3.13 , если

3.14 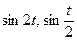, если

3.15 , если

3.16 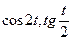, если

3.17 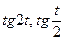, если

3.18 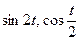, если

3.19 , если

3.20 , если

3.21 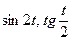, если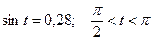

3.22 , если

3.23 , если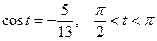

3.24 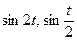, если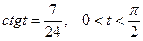

Задание 4. Вычислить:

4.1

4.2

4.3

4.4

4.5

4.6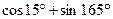

4.7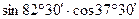

4.8

4.9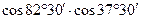

4.10

4.11

4.12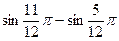

4.13

4.14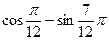

4.15

4.16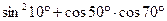

4.17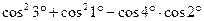

4.18

4.19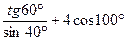

4.20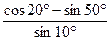

4.21

4.22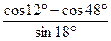

4.23

4.24

Задание 5

5.1 Найти , если .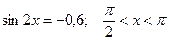

5.2 Вычислить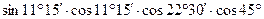

5.3 Найти , если .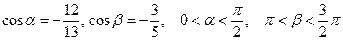

5.4 Найти .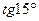

5.5 Найти .

5.6 Найти .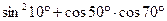

5.7 Вычислить , если .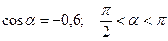

5.8 Вычислить .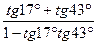

5.9 Найти , если .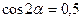

5.10 Вычислить .

5.11 Вычислить .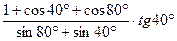

5.12 Вычислить 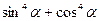, если .

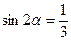5.13 Найти , если .

5.14 Найти , если .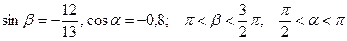

5.15 Вычислить .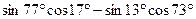

5.16 Вычислить .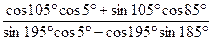

5.17 Найти .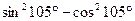

5.18 Найти , если .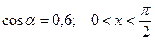

5.19 Найти 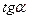, если .

5.20 Найти 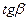, есл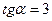и и .

5.21 Найти 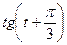, если .

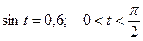5.22 Вычислить .

5.23 Вычислить . 5.24 Вычислить .

Дата добавления: 2014-11-29