Конус второго порядка

Определение 1. Конусом второго порядка называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат имеет вид

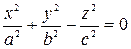(5.33)

(считаем, что в этом уравнии 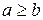). Начало координат, оси координат и координатные плоскости являются соответственно центром симметрии, осями симметрии и плоскостями симметрии и называются вершиной, главными осями и главными плоскостями. Осью конуса (5.33) обычно называют ось Oz.

Основное свойство конуса: если на конусе (5.33)лежит точка 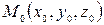(не совпадающая с вершиной), то на нем лежат все точки прямой 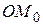, проходящей через вершину О и эту точку М ₀ (рис.3.16).

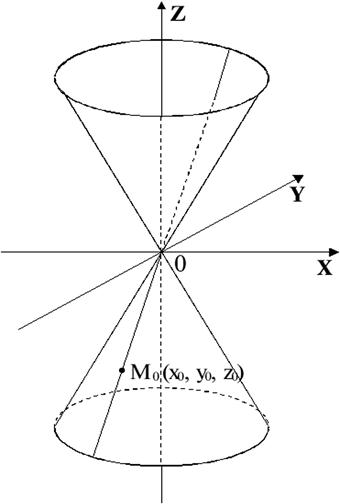
Рис. 3.16

В самом деле, если 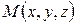– произвольная точка, лежащая на прямой 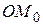, то 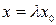, y=λy₀, 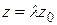и поэтому

,

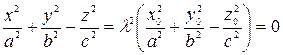а это значит, что точка принадлежит конусу.

Таким образом, поверхность (5.33) образована прямыми, проходящими через начало координат. Поэтому для представления вида этой поверхности достаточно рассмотреть ее сечение какой-нибудь плоскостью 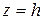, параллельной плоскости хОу. В сечении получится эллипс, уравнения которого

, .

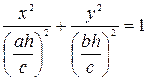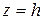Центр этого эллипса лежит на оси Oz в точке 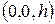, а значит, поверхность (5.33) образована прямыми, соединяющими начало координат со всеми точками эллипса (рис.3.16).

Исходя из основного свойства конуса второго порядка, дадим определение произвольной конической поверхности.

Определение 2. Конической поверхностью (или конусом) называется поверхность, образованная перемещением прямой, проходящей через одну и ту же точку и заданную кривую.

Перемещающаяся прямая называется образующей конуса, данная точка – вершиной, а заданная линия – направляющей.

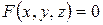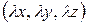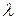По определению, уравнению конической поверхности должны удовлетворять координаты всех точек прямой образующей конуса, т.е. точки с координатами , где – любое действительное число; 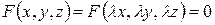, а это значит, что функция 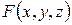в уравнении, задающем коническую поверхность, должна быть однородной.

Определение 3. Функция 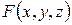называется однородной, если она обладает следующими свойствами:

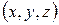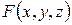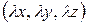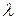1. Если точка входит в область определения функции , то точка , где – любое действительное число, также входит в область определения этой функции;

2. Существует такое число k, что для любой точки 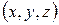из области определения функции 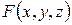и для любого числа 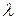выполняется соотношение

.

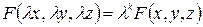Число k называется показателем (степенью) однородности. Для конуса второго порядка (5.33) показатель однородности k = 2.

Дата добавления: 2014-11-29