Эллиптический параболоид

Определение. Эллиптическим параболоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат имеет вид

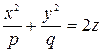, где . (5.34)

Будем считать, что 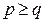. Если 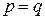, то эллиптический параболоид (5.34) – это параболоид вращения, так как он получается вращением параболы 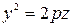вокруг оси Oz, являющейся осью параболы (рис.3.17).

Ось Oz является осью симметрии эллиптического параболоида (5.34) (она называется осью параболоида), а плоскости xOz и yOz – плоскостями симметрии (главные плоскости). Начало координат для эллиптического параболоида является точкой пересечения этой поверхности с ее осью и называется вершиной.

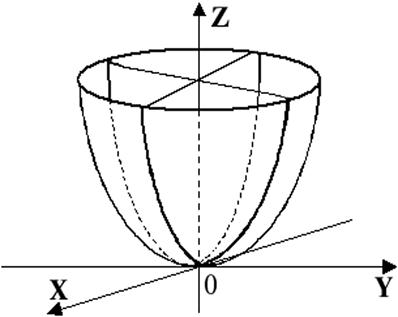
Рис. 3.17

Плоскость 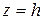пересекает эллиптический параболоид (5.34) по линии

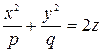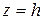, . (5.35)

Если 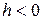, то первое уравнение не имеет действительных рещшений, так как ; это означает, что плоскость 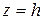при 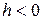не пересекает эллиптический параболоид. Если 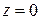, то 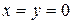, т.е. плоскость хОу имеет с эллиптическим параболоидом только одну общую точку – вершину 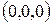. Если , то, переписав уравнение (5.35) в виде , ,

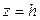видим, что сечением является эллипс с центром в точке 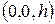и полуосям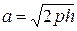и и .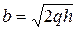

Плоскость xOz пересекает эллиптический параболоид (5.34) по параболе , у = 0, а плоскость yOz – по параболе 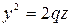, х = 0.

Таким образом, числа р и q – параметры парабол, получающихся в сечении параболоида его плоскостями симметрии (рис.3.17).

Рассмотрим сечения эллиптического параболоида плоскостями, параллельными плоскости xOz,т.е. плоскостями, заданные уравнением .

Уравнения линии сечения: 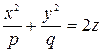, , или

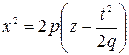, . (5.36)

Эти уравнения выражают параболу с вершиной в точке 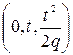, ось симметрии которой одинаково направлена с осью Oz. Параметр параболы (5.36) равен р, т.е. параметру главного сечения элиптического параболоида плоскостью xOz (при этом t = 0).

Таким образом, эллиптический параболоид может быть образован параллельным переносом параболы (5.36), при котором вершина этой параболы перемещается по параболе 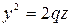, х = 0, полученной пересечением эллиптического параболоида плоскостью yOz. Следовательно, плоскости этих парабол перпендикулярны, а оси параллельны и одинаково направлены.

Аналогичная картина получается и для сечений эллиптического параболоида (5.34) плоскостями, параллельными плоскости yOz.

Дата добавления: 2014-11-29