Цилиндры второго порядка

Определение 1. Цилиндрической поверхностью называется поверхность, образованная параллельными между собой прямыми, называемыми ее образующими.

Если какая-нибудь плоскость, пересекающая все образующие цилиндрические поверхности, пересекает ее по линии Р, то эта линия называется направляющей этой цилиндрической поверхности.

Теорема. Если в пространстве введена декартова система координат и уравнение 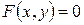в плоскости хОу является уравнением некоторой линии Р, то это уравнение в пространстве есть уравнение цилиндрической поверхности L с направляющей линией Р, а образующие параллельны оси Oz (рис.3.19, а).

Доказательство. Точка 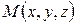лежит на цилиндрической поверхности L тогда и только тогда, когда проекция точки М на плоскость хОу параллельно оси Oz лежит на линии Р, т.е. тогда и только тогда, когда выполняется уравнение .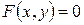

Рис. 3.19

Аналогичные заключения имеют место для уравнений вида 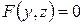(рис. 3.19, б) и (рис.3.19, в).

Определение 2. Цилиндрические поверхности, направляющими которых есть линии второго порядка, называются цилиндрическими поверхностями второго порядка.

Существуют три типа цилиндров второго порядка: эллиптический (рис.3.20)

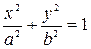, (5.42)

гиперболический (рис.3.21)

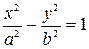, (5.43)

параболический (рис.3.22)

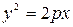. (5.44)

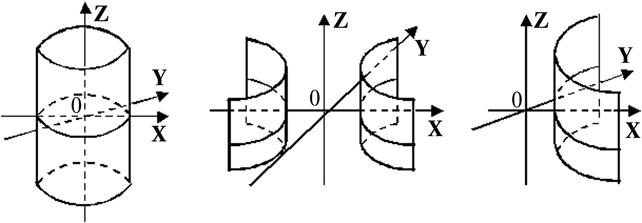
Рис. 3.20 Рис. 3.21 Рис. 3.22

Для цилиндров, заданных уравнениями (5.42), (5.43) и (5.44), направляющими линиями являются соответственно эллипс

,

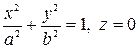гипербола

,

парабола

,

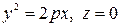а образующие параллельны оси Oz.

Замечание. Как мы видели, конические и цилиндрические поверхности второго порядка имеют прямолинейные образующие, причем каждая из этих поверхностей может быть образована движением прямой в пространстве.

Оказывается, что среди всех поверхностей второго порядка, кроме цилиндра и конуса, прямолинейными образующими обладают еще однополостный гиперболоид и гиперболический параболоид, причем, так же, как и в случае цилиндра и конуса, обе эти поверхности могут быть образованы движением прямой в пространстве (см. специальную литературу).

§4. ПРИВЕДЕНИЕ ОБЩЕГО УРАВНЕНИЯ ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА К КАНОНИЧЕСКОМУ ВИДУ

В общем уравнении поверхности второго порядка

(5.45)

содержатся следующие группы членов:

а) квадратичная форма

, (5.46)

где ;

б) линейная форма

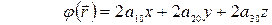, (5.47)

где ;

в) свободный член .

Чтобы привести уравнение (5.45) к каноническому виду, необходимо, в первую очередь, осуществить такое преобразование координат 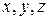, а, следовательно, и связанный с ней ортонормированный базис 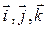, которое преобразует квадратичную форму (5.46) к каноническому виду (см. кн.2, гл.8, §3, п.3.1).

Матрица этой квадратичной формы имеет вид

,

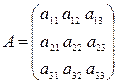где 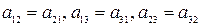, т.е. матрица А – симметрическая. Обозначим через 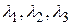собственные числа, а через 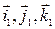ортонормированный базис, составленный из собственных векторов матрицы А. Пусть

–

матрица перехода от базиса 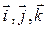к базису 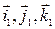, а 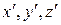– связанная с этим базисом новая система координат.

Тогда при преобразовании координат

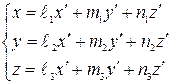(5.48)

квадратичная форма (5.46) примет канонический вид

,

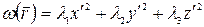где .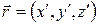

Теперь, применяя преобразование координат (5.48) к линейной форме (5.47), получим

,

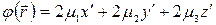где 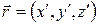, 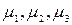– новые коэффициенты формы (5.47).

Таким образом, уравнением (5.45) принимает вид

+ .

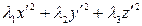Это уравнение может быть приведено к канонической форме с помощью параллельного переноса системы координат по формулам

или 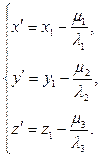(5.49)

После осуществления преобразования системы координат путем параллельного переноса (5.49), общее уравнение поверхности второго порядка (5.45) относительно декартовой системы координат 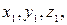будет выражать одну из следующих семнадцати поверхностей:

1) эллипсоид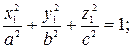

2) мнимый эллипсоид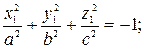

3) однополостный гиперболоид

4) двуполостной гиперболоид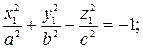

5) конус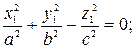

6) мнимый конус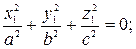

7) эллиптический параболоид

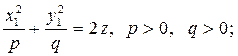
8) гиперболический параболоид

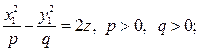
9) эллиптический цилиндр

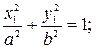
10) мнимый эллиптический цилиндр

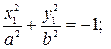
11) две мнимые пересекающиеся плоскости

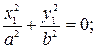
12) гиперболический цилиндр

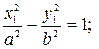
13) две пересекающиеся плоскости

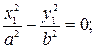
14) параболический цилиндр

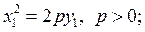
15) две параллельные плоскости

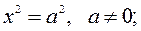
16) две мнимые параллельные плоскости

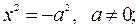
17) две совпадающие плоскости

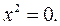
Пример. Определить вид и расположение поверхности, заданной относительно декартовой прямоугольной системы координат 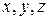и связанным с ней ортонормированным базисом 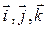уравнением

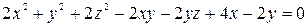(5.50)

Приведем квадратичную форму

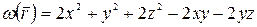(5.51)

к каноническому виду. Матрица этой формы имеет вид

.

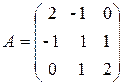Определим собственные числа этой матрицы из характеристического уравнения

.

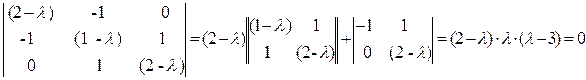Отсюда l ₁ = 2, l ₂ = 0, l₃ = 3.

Теперь находим собственные векторы матрицы А: 1) пусть 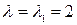, тогда из уравнения 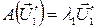или в координатной форме

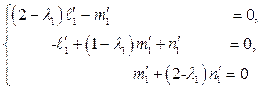
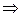
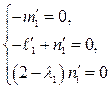
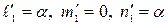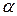находим , где – любое число, и, следовательно, , а 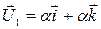. Из всего множества коллинеарных векторов 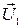выбираем вектор 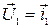, модуль которого , т.е. нормируем вектор .

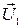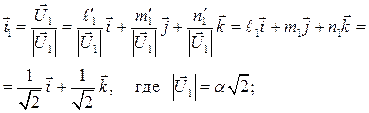
2) для 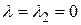имеем

.

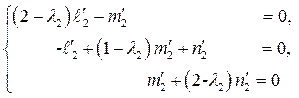
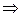
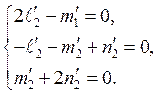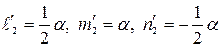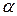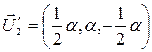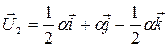Отсюда , где – любое число. Тогда , а . Нормируя вектор 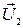, находим единичный вектор 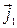для направления, задаваемого вектором :

,

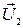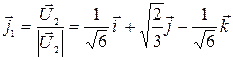где .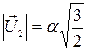

3) 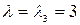, тогда для компонент 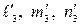вектора 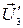имеем систему

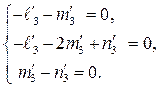
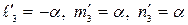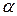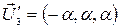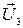Откуда , где – любое число, и, следовательно, , а . Нормируя вектор , находим единичный вектор для направления, задаваемого вектором :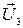

,

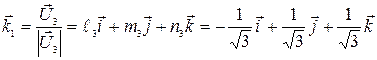где .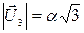

Перейдем теперь от ортонормированного базиса 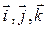к ортонормированному базису 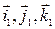, составленного из собственных векторов матрицы А и свяжем с последним базисом новую декартову прямоугольную систему координат 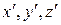. Матрица перехода для такого преобразования имеет вид

,

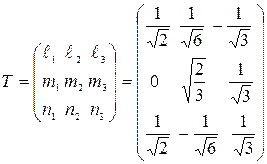а координаты преобразуются по формулам

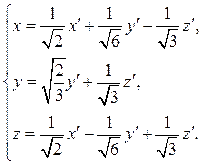(5.52)

Применяя данное преобразование координат к квадратичной форме (5.51), приведем ее к каноническому виду

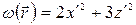, где .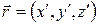

Определим теперь, какой вид имеет линейная формула

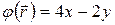, где ,

если координаты преобразуются по формулам (5.52). Имеем

.

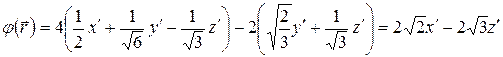Таким образом, если систему координат 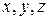преобразовать по формулам (5.52), то относительно новой системы координат 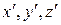рассматриваемая поверхность второго порядка задается уравнением

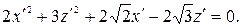(5.53)

Уравнение (5.53) приводим к канонической форме с помощью параллельного переноса системы координат по формулам

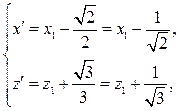
после чего, уравнение поверхности относительно системы координат 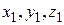принимает вид

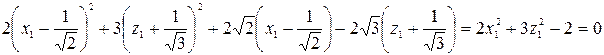
или

Это уравнение выражает эллиптический цилиндр, направляющий эллипс которого расположен в координатной плоскости 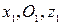, а образующие прямые параллельны оси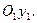

Замечание. Схема приведения общего уравнения поверхности второго порядка к каноническому виду, изложенная в этом параграфе, может быть примененена и к приведению общего уравнения кривой второго порядка к каноническому виду.

Дата добавления: 2014-11-29