Гиперболический параболоид

Определение. Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой спкциально выбранной прямоугольной системе координат имеет вид

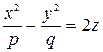, где 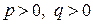. (5.37)

Для гиперболического параболоида (5.37) плоскости xOz и yOz являются плоскостями симметрии, а ось Oz – осью симметрии.

Ось симметрии гиперболического параболоида называется просто его осью. Точка, в которой ось гиперболического параболоида пересекает эту поверхность, называется вершиной. Гиперболический параболоид (5.37) имеет вершину в начале координат.

Плоскости xOz и yOz, являющиеся для гиперболического параболоида (5.37) плоскостями симметрии, называются главными плоскостями гиперболического параболоида.

Гиперболический параболоид (5.37) в случае 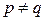имеет только одну ось симметрии (ось Ох), если же 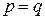, то параболоид имеет еще две оси симметрии: и .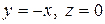

В самом деле, если координаты точки 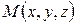удовлетворяют уравнению , то этому же уравнению удовлетворяют координаты точки 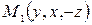, симметричной с точкой 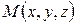относительно прямой . Так же доказывается, что прямая 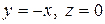является осью симметрии.

Плоскость хОу пересекает гиперболический параболоид по двум прямым:

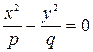, или ,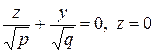

и

.

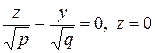Плоскость 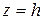, параллельная плоскости хОу,пересекает гиперболический параболоид по гиперболе (рис.3.18, а)

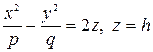. (5.38)

Если 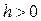, то эти уравнения можно переписать в виде

.

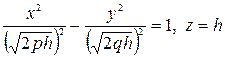Это гипербола, расположенная в плоскости 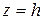с центром в точке 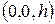, действительная ось которой параллельна оси Ох, а мнимая – параллельна оси Оу.

Если 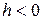, то уравнения линии сечения можно представить в виде

.

Это гипербола, расположенная в плоскости 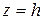с центром в точке 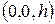, действительная ось которой параллельна оси Оу, а мнимая – параллельна оси Ох. Асимптоты всех гипербол, получающихся при пересечении гиперболического параболоида (5.37) плоскостями 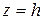, , параллельны прямым, по которым этот параболоид пересекается с плоскостью .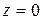

Рис. 3.18

Плоскость xOz пересекает гиперболический параболоид по параболе (рис.3.18, б)

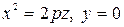, (5.39)

а плоскость – по параболе

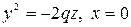. (5.40)

Таким образом, числа p и q являются параметрами парабол, получающихся в сечении гиперболического параболоида (5.37) его главными плоскостями.

Рассмотрим сечения гиперболического параболоида (5.37)плоскостями, параллельными плоскости (рис.3.18, б), т.е. плоскостями, выраженными уравнением .

Уравнения линии сечения имеют вид

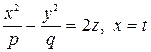, или .

Эти уравнения выражают параболу с вершиной в точке 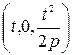, ось которой выражается уравнениями , у = 0, а направление оси совпадает с отрицательным направлением оси Oz. Параметр параболы

(5.41)

равен q, т.е. параметру главного сечения (5.40) гиперболического параболоида плоскостью yOz (t = 0).

Таким образом, гиперболический параболоид может быть образован параллельным переносом параболы (5.41), при котором вершина параболы (5.41) перемещается по параболе (5.39); плоскость параболы (5.39) перпендикулярна плоскости параболы (5.41), а оси этих парабол параллельны и противоположно направлены (рис.3.18, б).

Аналогичная картина получается и для сечений гиперболического параболоида плоскостями, параллельными плоскости xOz.

Гиперболический параболоид называют иногда седлообразной поверхностью.

Дата добавления: 2014-11-29