Основные сведения о структуре механических систем оборудования

Основные сведения о структуре фасовочно-упаковочного оборудования и его основных механизмах

Лекция 9

9.1.Основные сведения о структуре механических систем оборудования

9.2.Виды передач и механизмов кинематических цепей фасовочно-упаковочного оборудования

9.3.Понятие о структурном анализе и синтезе механизмов

Условные обозначения

Глоссарий

Контрольные вопросы

Механика рассматривает движение и равновесие отдельных материальных точек и механических систем, состоящих из совокупности этих точек под действием внешних сил.

Механические системы делятся на геометрически изменяемые и геометрически неизменяемые. Примерами геометрически неизменяемых систем являются:

- деталь, деформацией которой можно пренебречь;

- звено – деталь или несколько неподвижно соединенных между собой деталей;

- ферма – несколько деталей (стержней), связанных между собой так, что исключается их относительные движения.

Геометрически изменяемую систему представляет кинематическая цепь, составляющие элементы (звенья) которой связаны между собой подвижными соединениями (кинематическими парами) так, что могут перемещаться относительно друг друга. Изменяемые системы используются в качестве механизмов. Элементарный механизм представляет собой кинематическую цепь, состоящую из одного неподвижно закрепленного звена (стойки), в которой при заданном движении одного ведущего звена все остальные звенья получают определенные движения. Для обеспечения определенности движения звеньев при одном ведущем звене и отсутствии избыточных связей необходимо, чтобы число степеней свободы механизма равнялось единице .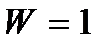

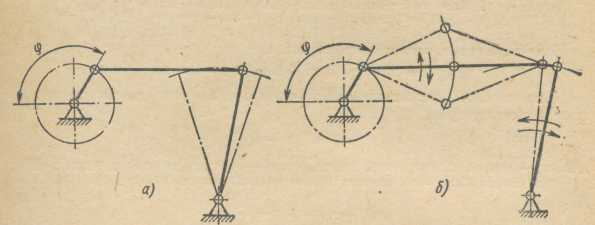
Число степеней свободы механизма равно числу независимо изменяемых координат положений его звеньев. Например, в шарнирном четырехзвенном механизме (рис.9.1а) 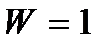, так как независимо может меняться только угол поворота кривошипа 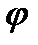. При 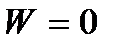звенья механизма неподвижны, при 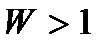появляется неопределенность движенья звеньев.

Рис. 9.1 Схемы шарнирных механизмов (а) - 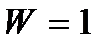, (б) -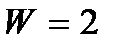

Число степеней свободы плоских механизмов определяется по формул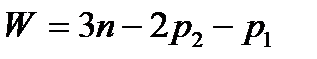е , где 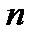- число подвижных звеньев (стойка не учитывается), 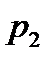- число вращательных, поступательных и других кинематических пар, допускающих движение одного звена относительно другого с одной степенью свободы, 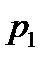- число кинематических пар, допускающих движение одного звена относительно другого с .

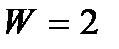Так для механизма, указанного на рис. 9.1.а .

Для плоского механизма, звенья которого могут двигаться только поступательно число степеней свободы вычисляется по формуле 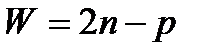, где - число подвижных звеньев, 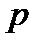- число кинематических пар

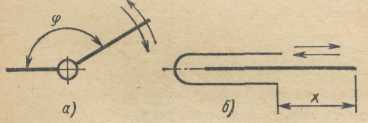
На рис. 9.2 приведены примеры кинематических пар, допускающих относительное движенье звеньев с 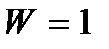: (а) – вращательная пара, в которой изменяется только одна координата – угол 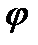(б) – поступательная пара, где изменяется одна координата .

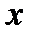Рис.9.2 Примеры кинематических пар с одной степенью свободы, (а) – вращательная пара, (б) – поступательная пара

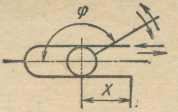
Пример кинематической пары, допускающей относительное движение с двумя степенями свободы, показан на рис. 9.3.

Рис.9.3 Кинематическая пара с двумя степенями свободы

Избыточными (пассивными) связями в механизмах называют такие связи, которые устраняют возможность тех относительных движений звеньев, уже исключенных другими связями. Число пассивных связей в плоском механизме определяется разностью между фактическим значением 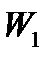механизма и подсчитанным по формуле 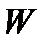, т.е. .

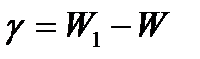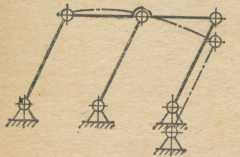
На рис. 9.4. приведен пример статически неопределимого механизма – двойного шарнирного параллелограмма, у которого 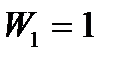, а 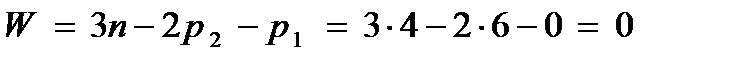. Поэтому .

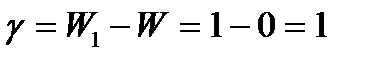Рис.9.4 Схема статически неопределимого механизма

Пассивные связи вводятся в механизмы для увеличения нагрузочной способности или, как в примере (рис.9.4), для увеличения жесткости. Однако введение пассивных связей делает механизм статически неопределимым со степенью статической неопределимости равной .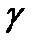

Статически неопределимой системой называется такая система, для которой уравнений равновесия статики недостаточно, чтобы определить все силы и моменты, нагружающие элементы системы и их соединения. Статическая неопределимость приводит к необходимости точного соблюдения размеров звеньев, что достигается назначением жестких допусков, пригонкой, введением компенсаторов или регулировочных устройств. Неувязка в размерах может привести к деформации звеньев из-за дополнительного нагружения деталей и к неработоспособности механизма. При силовом анализе статически неопределимых систем следует учитывать деформацию деталей и принимать различные допущения в расчетных схемах таких механизмов.

В геометрически неизменяемой системе (ферме) составляющие элементы связаны без возможности перемещения относительно друг друга. Неизменяемые системы используют в виде самостоятельных сооружений или в составе механизма в качестве подвижного отдельного звена.

Дата добавления: 2014-11-29