Для проверки статистической значимости коэффициентов регрессии используется случайная величина 2 страница

Р _прогн = 53, W _прогн = 4, = 0,03.

Вариант 1.4

Q

P

W

Р _прогн = 28, W _прогн = 9, = 0,04.

Вариант 1.5

Q

P

W

Р _прогн = 25, W _прогн = 12, = 0,05.

Задача 2. Для объяснения изменения ВНП за 10 лет строится регрессионная модель с объясняющими переменными – потреблением (С) и инвестициями (I):

ВНП = ₀ + ₁ С + ₂ I + .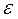

Статистические данные приведены в таблице.

Задание.

1. По МНК оценить коэффициенты линейной регрессии _i, i = 0, 1, 2;

2. Оценить статистическую значимость найденных эмпирических коэффициентов регрессии b_i, i =0, 1, 2;

3. В соответствие с заданным значением построить доверительные интервалы для найденных коэффициентов;

4. Вычислить коэффициент детерминации R ² и оценить его статистическую значимость при заданном значении ;

5. Определить какой процент разброса зависимой переменной объясняется данной регрессией;

6. Сравнить коэффициент детерминации R ² со скорректированным коэффициентом детерминации;

7. Вычислить статистику DW Дарбина-Уотсона и оценить наличие автокорреляции;

8. Посредством коэффициентов b_i, i = 1, 2, оценить в % отношении влияние объясняющих переменных С и I на изменение объясняемой переменной;

9. Спрогнозировать значение объясняемой переменной ВНП _прогн для прогнозных значений С _прогн, I _прогн и определить доверительный интервал для ВНП_прогн;

10. Сделать обобщающие выводы по регрессионной модели.

Вариант 2.1

С, млрд $	8,0	9,5	11,0	12,0	13,0	14,0	15,0	16,5	17,0	18,0
I, млрд $	1,65	1,8	2,0	2,1	2,2	2,4	2,65	2,85	3,2	3,55
ВНП, млрд $	14,0	16,0	18,0	20,0	23,0	23,5	25,0	26,5	28,5	30,5

С _прогн = 20, I _прогн = 4, = 0,02.

Вариант 2.2

С, млрд $	5,0	6,5	6,9	7,5	8,0	10,0	11,0	12,0	14,0	17,0
I, млрд $	1,2	1,4	1,6	1,9	2,0	2,4	2,5	2,7	3,0	3,4
ВНП, млрд $	10,0	10,5	11,0	13,0	14,0	15,0	18,0	21,0	24,0	28,0

С _прогн = 20, I _прогн = 4, = 0,03.

Вариант 2.3

С, млрд $	7,0	8,0	9,0	10,5	11,0	12,5	13,0	14,0	15,0	16,0
I, млрд $	1,2	1,4	1,5	1,6	1,8	2,0	2,2	2,4	2,7	2,9
ВНП, млрд $	12,0	14,0	15,0	16,0	18,0	22,0	23,0	23,5	25,0	26,0

С _прогн = 14,5, I _прогн = 3, = 0,04.

Вариант 2.4

С, млрд $	6,0	7,5	9,0	10,0	11,0	12,0	13,0	14,0	15,6	16,8
I, млрд $	1,4	1,5	1,7	1,8	2,0	2,1	2,2	2,4	2,6	3,0
ВНП, млрд $	11,0	13,0	15,0	16,0	18,0	20,0	23,0	23,5	25,0	26,5

С _прогн = 18,0, I _прогн = 3,2, = 0,05.

Вариант 2.5

С, млрд $	9,0	10,5	12,0	13,0	14,0	15,0	16,5	17,5	18,0	18,5
I, млрд $	1,4	1,6	2,1	2,2	2,4	2,7	2,9	3,3	3,6	4,0
ВНП, млрд $	13,0	16,0	20,0	23,0	23,5	25,0	27,0	29,0	31,0	33,0

С _прогн = 19,0, I _прогн = 4,0, = 0,06.

Задача 3. В таблице даны статистические данные о расходах на питание Y, душевом доходе Х₁ и размере семьи Х₂ для девяти групп семей. Построить регрессионную модель:

Y = ₀ + ₁ Х ₁ + ₂ Х ₂ + .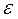

Задание.

1. По МНК оценить коэффициенты линейной регрессии _i, i = 0, 1, 2.

2. Оценить статистическую значимость найденных эмпирических коэффициентов регрессии b_i, i =0, 1, 2.

3. В соответствие с заданным значением построить доверительные интервалы для найденных коэффициентов;

4. Вычислить коэффициент детерминации R ² и оценить его статистическую значимость при заданном значении ;

5. Определить какой процент разброса зависимой переменной объясняется данной регрессией;

6. Сравнить коэффициент детерминации R ² со скорректированным коэффициентом детерминации;

7. Вычислить статистику DW Дарбина-Уотсона и оценить наличие автокорреляции;

8. Посредством коэффициентов b_i, i = 1, 2, оценить в % отношении влияние объясняющих переменных Х ₁ и Х ₂ на изменение объясняемой переменной;

9. Спрогнозировать значение объясняемой переменной Y_прогн для прогнозных значений Х _{1 прогн}, Х _{2 прогн} и определить доверительный интервал для Y _прогн;

10. Сделать обобщающие выводы по регрессионной модели.

Вариант 3.1

№	Расход на питание Y, у.е.	Душевой доход Х 1, у.е.	Размер семей Х 2
			1,4
			2,0
			2,5
			3,1
			3,2
			3,4
			3,6
			3,9
			3,6

Х _{1 прогн} = 8000, Х _{2 прогн} = 4,0, = 0,01.

Вариант 3.2

№	Расход на питание Y, у.е.	Душевой доход Х 1, у.е.	Размер семей Х 2
			1,2
			2,0
			2,4
			2,4
			3,0
			3,2
			3,4
			3,6
			3,6

Х _{1 прогн} = 10000, Х _{2 прогн} =3,0, = 0,02.

Вариант 3.3

№	Расход на питание Y, у.е.	Душевой доход Х 1, у.е.	Размер семей Х 2
			1,0
			1,6
			2,0
			2,0
			2,3
			2,8
			3,0
			3,2
			3,6

Х _{1 прогн} = 8000, Х _{2 прогн} =3,0, = 0,03.

Вариант 3.4

№	Расход на питание Y, у.е.	Душевой доход Х 1, у.е.	Размер семей Х 2
			1,1
			1,8
			2,0
			2,1
			2,4
			2,4
			2,6
№	Расход на питание Y, у.е.	Душевой доход Х 1, у.е.	Размер семей Х 2
			3,0
			3,0

Х _{1 прогн} = 13000, Х _{2 прогн} =3,2, = 0,04.

Вариант 3.5

№	Расход на питание Y, у.е.	Душевой доход Х 1, у.е.	Размер семей Х 2
			1,7
			2,0
			2,4
			2,8
			2,9
			3,0
			3,1
			3,0
			3,5

Х _{1 прогн} = 11000, Х _{2 прогн} =3,0, = 0,05.

Задача 4. Изучается влияние стоимости основных и оборотных средств на величину валового дохода торговых предприятий. Для этого по 12 торговым предприятиям были получены данные приведенные в таблице. Построить регрессионную модель:

Y = ₀ + ₁ Х ₁ + ₂ Х ₂ + .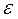

Задание.

1. По МНК оценить коэффициенты линейной регрессии _i, i = 0, 1, 2.

2. Оценить статистическую значимость найденных эмпирических коэффициентов регрессии b_i, i =0, 1, 2.

3. В соответствие с заданным значением построить доверительные интервалы для найденных коэффициентов;

4. Вычислить коэффициент детерминации R ² и оценить его статистическую значимость при заданном значении ;

5. Определить какой процент разброса зависимой переменной объясняется данной регрессией;

6. Сравнить коэффициент детерминации R ² со скорректированным коэффициентом детерминации;

7. Вычислить статистику DW Дарбина-Уотсона и оценить наличие автокорреляции;

8. Посредством коэффициентов b_i, i = 1, 2, оценить в % отношении влияние объясняющих переменных Х ₁ и Х ₂ на изменение объясняемой переменной;

9. Спрогнозировать значение объясняемой переменной Y _прогн для прогнозных значений Х _{1 прогн}, Х _{2 прогн} и определить доверительный интервал для Y _прогн;

10. Сделать обобщающие выводы по регрессионной модели.

Вариант 4.1

Номер предприятия	Валовый доход за год, млн.руб.	Среднегодовая стоимость, млн.руб.
Основных фондов	Оборотных средств

Х _{1 прогн} = 140, Х _{2 прогн} =58, = 0,01.

Вариант 4.2

Номер предприятия	Валовый доход за год, млн.руб.	Среднегодовая стоимость, млн.руб.
Основных фондов	Оборотных средств

Х _{1 прогн} = 150, Х _{2 прогн} =100, = 0,02.

Вариант 4.3

Номер предприятия	Валовый доход за год, млн.руб.	Среднегодовая стоимость, млн.руб.
Основных фондов	Оборотных средств

Х _{1 прогн} = 100, Х _{2 прогн} =80, = 0,03.

Вариант 4.4

Номер предприятия	Валовый доход за год, млн.руб.	Среднегодовая стоимость, млн.руб.
Основных фондов	Оборотных средств

Х _{1 прогн} = 90, Х _{2 прогн} =50, = 0,04.

Вариант 4.5

Номер предприятия	Валовый доход за год, млн.руб.	Среднегодовая стоимость, млн.руб.
Основных фондов	Оборотных средств

Х _{1 прогн} = 50, Х _{2 прогн} =60, = 0,05.

Задача 5. Имеются данные по странам за 2005 год. Построить регрессионную модель:

Y = ₀ + ₁ Х ₁ + ₂ Х ₂ + .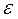

Задание.

1. По МНК оценить коэффициенты линейной регрессии _i, i = 0, 1, 2.

2. Оценить статистическую значимость найденных эмпирических коэффициентов регрессии b_i, i =0, 1, 2.

3. В соответствие с заданным значением построить доверительные интервалы для найденных коэффициентов;

4. Вычислить коэффициент детерминации R ² и оценить его статистическую значимость при заданном значении ;

5. Определить какой процент разброса зависимой переменной объясняется данной регрессией;

6. Сравнить коэффициент детерминации R² со скорректированным коэффициентом детерминации;

7. Вычислить статистику DW Дарбина-Уотсона и оценить наличие автокорреляции;

8. Посредством коэффициентов b_i, i = 1, 2, оценить в % отношении влияние объясняющих переменных Х ₁ и Х ₂ на изменение объясняемой переменной;

9. Спрогнозировать значение объясняемой переменной Y _прогн для прогнозных значений Х _{1 прогн}, Х _{2 прогн} и определить доверительный интервал для Y _прогн;

10. Сделать обобщающие выводы по регрессионной модели.

Вариант 5.1

Страна	Индекс человеческого развития, Y	Ожидаемая продолжительность жизни при рождении 2005 г., лет, Х 1	Суточная калорийность питания населения, ккал на душу, Х 2
Австрия	0,904	77,0
Австралия	0,922	78,2
Аргентина	0,827	72,9
Белоруссия	0,763	68,0
Бельгия	0,923	77,2
Бразилия	0,739	66,8
Великобритания	0,918	77,2
Венгрия	0,795	70,9
Германия	0,906	77,2

Х _{1 прогн} = 80, Х _{2 прогн} =3500, = 0,01.

Вариант 5.2

Страна	Индекс человеческого развития, Y	Ожидаемая продолжительность жизни при рождении 2005 г., лет, Х 1	Суточная калорийность питания населения, ккал на душу, Х 2
Греция	0,867	78,1
Дания	0,905	75,7
Египет	0,616	66,3
Израиль	0,883	77,8
Индия	0,545	62,6
Испания	0.894	78,0
Италия	0,900	78,2
Канада	0,932	79,0
Казахстан	0,740	67,7

Х _{1 прогн} = 75, Х _{2 прогн} =3000, = 0,02.

Вариант 5.3

Страна	Индекс человеческого развития, Y	Ожидаемая продолжительность жизни при рождении 2005 г., лет, Х 1	Суточная калорийность питания населения, ккал на душу, Х 2
Китай	0,701	69,8
Латвия	0,744	68,4
Нидерланды	0,921	77,9
Норвегия	0,927	78,1
Польша	0,802	72,5
Корея	0,852	72,4
Россия	0,747	66,6
Румыния	0,752	69,9
США	0,927	76,6

Х _{1 прогн} = 72, Х _{2 прогн} =3500, = 0,03.

Вариант 5.4

Страна	Индекс человеческого развития, Y	Ожидаемая продолжительность жизни при рождении 2005 г., лет, Х 1	Суточная калорийность питания населения, ккал на душу, Х 2
Турция	0,728	69,0
Украина	0,721	68,8
Финляндия	0,913	76,8
Франция	0,918	78,1
Чехия	0,833	73,9
Швейцария	0,914	78,6
Швеция	0,923	78,5
ЮАР	0,695	64,1
Япония	0,924	80,0

Дата добавления: 2014-11-29