Неинерциальные системы отсчета. Силы инерции

В предыдущем было показано, что основное уравнение динамики Ньютона справедливо только в инерциальных системах отсчета. Между тем имеется много случаев, когда решение интересующей нас задачи необходимо получить в неинерциальных системах (например, движение математического маятника в ускоренно движущемся вагоне, движение спутника относительно поверхности Земли и др.). Поэтому возникает вопрос: как следует изменить основное уравнение динамики, чтобы оно оказалось справедливым и для неинерциальных систем отсчета?

С этой целью возьмем две системы отсчета: инерциальную K - систему и неинерциальную K¹ - систему. Пусть известны масса частицы т, сила действующая на нее со стороны каких-то определенных тел, и характер движения K¹ - системы относительно K -системы.

Рассмотрим сразу достаточно общий случай, когда K¹ - система вращается с постоянной угловой скоростью 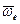вокруг оси, перемещающейся поступательно с ускорением относительно K - системы. Воспользуемся формулой преобразования ускорений (3.31). Из нее следует, что ускорение частицы в K' – системе

. (4.17)

Умножив обе части (4.17) на массу частицы т и учтя, что в инерциальной K - системе отсчета (согласно второму закону Ньютона), получим

. (4.18)

Это и есть основное уравнение динамики в неинерциальной К'- системе отсчета, которая вращается с постоянной угловой скоростью 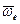вокруг оси, перемещающейся поступательно с ускорением . Из него видно, что даже при 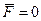частица будет двигаться в K '-системе с ускорением, в общем случае отличным от нуля, причем так, как если бы на нее действовали некоторые силы, соответствующие последним трем членам уравнения (4.18). Эти силы назвали силами инерции.

Перепишем уравнение (4.18) в таком виде:

, (4.19)

где

(4.20)

Здесь 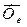- сила инерции, обусловленная поступательным движением системы отсчета, a - так называемая кориолисова сила инерции, обусловленная вращательным движением системы отсчета. Существенно, что все силы инерции, подобно силам тяжести, пропорциональны массе частицы.

Из предыдущего следует, что введение сил инерции позволяет сохранить по форме основное уравнение динамики и для неинерциальных систем отсчета: слева - произведение массы на ускорение, справа - силы. Но кроме сил, обусловленных действием определенных тел на данную частицу (сил взаимодействия), необходимо учесть и силы инерции, вид которых дается формулами (4.20).

Для сил инерции нельзя указать источник в виде определенного тела, действующего на рассматриваемую частицу. Поэтому силы инерции не имеют противодействующих, и в отличие от сил взаимодействия не подчиняются третьему закону Ньютона.

Именно в силу этих обстоятельств силы инерции часто называют фиктивными, в связи с чем нередко возникают разногласия к относительно истинности этих сил. Следует, однако, иметь в виду, что с этими разногласиями не связано никакой физической проблемы, а речь идет по существу, лишь о недоразумениях, возникающих вследствие нечеткой терминологии. Термин «фиктивная сила» вряд ли можно считать удачным, потому что силы инерции имеют совершенно определенный физический смысл: они существуют только в неинерциальных системах отсчета. В инерциальных системах их просто нет.

Возникновение и действие сил инерции можно проследить на следующем простом примере.

Задача 4.7

На поверхности стола находится горизонтальный диск D, который свободно вращается вокруг вертикальной оси с постоянной угловой скоростью . Над диском висит шарик массы т, как показано на рис. 4.7,а. Рассмотрим поведение этого шарика в. K - системе отсчета, связанной со столом (она предполагается инерциальной), и в K^/ – системе, связанной с вращающимся диском.

Решение. В инерциальной K - системе на шарик действуют две силы: сила тяжести и сила натяжения со стороны нити. Эти силы компенсируют друг друга, и шарик покоится в K - системе.

В неинерциальной K^/ - системе шарик движется равномерно по окружности с нормальным ускорением 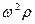, где ρ - расстояние от шарика до оси вращения. Легко убедиться, что это ускорение обусловлено действием сил инерции. Действительно, в К,' - системе, помимо указанных выше двух сил, компенсирующих друг друга, действуют еще центробежная сила инерции и сила Кориолиса (рис. 4.7,б). Взяв проекции этих сил на нормаль 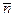к траектории в точке нахождения шарика, запишем согласно (4.19) и (4.20):

,

где учтено, что в данном случае v' = ω² ρ. Отсюда сразу видно,

что а'_n = ω² ρ.

Ранее было отмечено, что система отсчета, связанная с земной поверхностью, во многих случаях может считаться практически инерциальной. Однако существует ряд явлений, истолкование которых в этой системе отсчета невозможно без учета ее неинерциальности.

Известно, например, что ускорение свободного падения тел относительно поверхности Земли имеет наименьшее значение у полюсов. Уменьшение этого ускорения по мере приближения к экватору объясняется не только несферичностью Земли, но и возрастающим действием центробежной силы инерции. Или такие явления, как отклонение свободно падающих тел к востоку, размыв правых берегов рек в северном полушарии и левых берегов - в южном, вращение плоскости качания маятника Фуко и др. Подобные явления связаны с движением тел относительно поверхности Земли и могут быть объяснены действием сил Кориолиса.

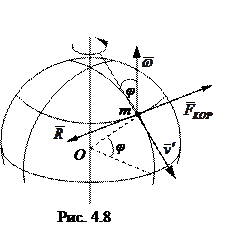Задача 4.8

Поезд массы т движется по меридиану на широте φ со скоростью v¹. Найти силу бокового давления, с которой поезд действует на рельсы.

Решение. В системе отсчета, связанной с Землей (она вращается с угловой скоростью ), составляющая ускорения поезда, перпендикулярная плоскости меридиана, равна нулю. Поэтому и сумма проекций сил, действующих на поезд в этом направлении, также равна нулю. А это значит, что сила Кориолиса 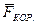(рис. 4.8) должна уравновешиваться силой 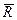бокового давления, действующей на поезд со стороны правого по ходу движения рельса, т. е. .

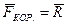По третьему закону Ньютона, поезд будет действовать на этот рельс в горизонтальном направлении с силой . Следовательно,

.

Модуль вектора в соответствии с рис. 4.8 равен .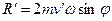

В заключение необходимо отметить, что любую механическую задачу можно решить как в инерциальной, так и в неинерциальной системах отсчета. Выбор той или иной системы отсчета обычно диктуется или постановкой вопроса, или стремлением получить решение возможно более простым путем. При этом часто наиболее удобно пользоваться именно неинерциальными системами отсчета.

Вывод

На основании трудов Галилея и Ньютона дано определение массе в её обоих известных проявлениях. Перечислены основные механические силы. Рассмотрено поведение системы тел в инерциальной и неинерциальной системах отсчёта. Определена сила инерции. Записано основное уравнение динамики для различных задач и координатных осей.

Контрольные вопросы

1. Сформулируйте законы Ньютона.

2. Дайте определение силе инерции и особенности её использования в решении задач.

3. Укажите различие инерциальной и неинерциальной систем отсчёта.

Глава 5 ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ

Дата добавления: 2014-11-29