Закон сохранения энергии частицы

Кинетическая энергия. Пусть частица массы т движется под действием некоторой силы (в общем случае сила может быть результирующей нескольких сил). Найдем элементарную работу, которую совершает эта сила на элементарном перемещении 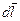. Имея в виду, что и 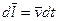, запишем

.

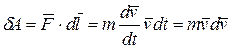Скалярное произведение , где 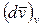- проекция вектора 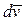на вектор . Эта проекция, очевидно, равна dv - приращению модуля вектора скорости. Поэтому 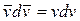и

.

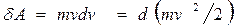Отсюда видно, что работа результирующей силы идет на приращение некоторой величины (стоящей в скобках) которую называют кинетической энергией Т.

. (5.17)

Таким образом, приращение кинетической энергии при элементарном перемещении равно

(5.18)

а при конечном перемещении из точки 1 в точку 2

(5.19)

Последние две формулы выражают закон изменения кинетической энергии частицы: приращение кинетической энергии частицы на некотором перемещении равно алгебраической сумме работ всех сил, действующих на частицу на том же перемещении. Если А ₁₂ > 0, то Т₂ > Т₁, т. е. кинетическая энергия частицы увеличивается; если же А ₁₂ < 0, то кинетическая энергия уменьшается. Закон изменения кинетической энергии можно представить и в другой форме, поделив обе части (5.18) на соответствующий промежуток времени dt:

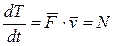(5.20)

Это значит, что производная кинетической энергии частицы по времени равна мощности N результирующей силы , действующей на частицу.

Задача 5.1

Небольшой брусок массы m скользит вниз по наклонной плоскости, составляющей угол α с горизонтом. На пути l скорость бруска меняется от v₁ до v₂. Коэффициент трения на всем пути один и тот же. Найти работу силы трения, действующей на брусок на пути l, а также среднюю мощность этой силы на данном пути.

Согласно (5.19), приращение кинетической энергии бруска на пути l равно Т₂ – Т₁ = A_mg+ A _ТР + A_R, где справа записаны работы всех сил, действующих на брусок: силы тяжести, силы трения и силы нормальной реакции со стороны наклонной плоскости. В данном случае A_mg = mgsinα l и A_R= 0 Поэтому

.

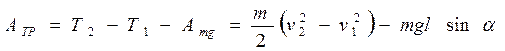Средняя мощность силы трения равна отношению работы этой силы к промежутку времени, за который совершается данная работа: N_СР. = A_ТР / Δ t = F_ТР l/ Δ t. Отношение l /Δ t равно средней скорости v_СР. В данном случае скорость меняется линейно, ибо силы, а значит, и ускорение бруска постоянны. Поэтому v _СР = (v₁ + v₂)/2. В результате получим

.

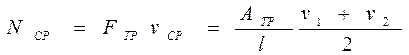В неинерциальной системе отсчета закон изменения кинетической энергии имеет тот же вид, что и (5.19) или (5.20). Но здесь, кроме сил, действующих на рассматриваемую частицу со стороны других тел (сил взаимодействия), необходимо учесть и действие сил инерции. Поэтому результирующая сила 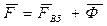, и работа этой силы А = А_ВЗ + А_Ф. Тогда формулы (5.19) и (5.20) можно представить в следующем виде

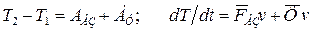, (5.21)

где все величины берутся относительно неинерциальной системы отсчета.

Задача 5.2

Горизонтально расположенный гладкий стержень вращается с постоянной угловой скоростью вокруг вертикальной оси, проходящей через один из его концов. Вдоль стержня без трения скользит небольшая муфта массы т. Когда муфта находилась Y оси вращения, ее скорость была равна нулю. Найти кинетическую энергию муфты относительно стержня в зависимости от расстояния ее до оси вращения.

Во вращающейся системе отсчета на муфту действуют четыре силы: сила тяжести, сила реакции со стороны стержня, сила Кориолиса и центробежная сила инерции. Первые три силы работы не совершают (они перпендикулярны к перемещению муфты), поэтому приращение кинетической энергии муфты обусловлено только работой центробежной силы инерции. Элементарная работа этой силы на перемещении dr равна δA _ЦБ= F_ЦБ dr = m ω² rdr. Интегрируя это выражение, получим в соответствии с (5.27)

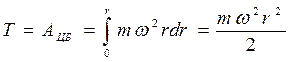
Полная механическая энергия частицы. Согласно (5.18), приращение кинетической энергии частицы равно элементарной работе результирующей всех сил, действующих на частицу. Что это за силы? Если частица находится в потенциальном поле, то на нее действует консервативная сила 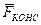со стороны потенциального поля. Кроме того, на частицу могут действовать и другие силы, имеющие иное происхождение. Назовем их сторонними силами . К числу сторонних сил относятся, например, силы трения и сопротивления, силы инерции и др. Таким образом, результирующая всех сил, действующих на частицу, может быть представлена в виде 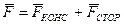. Работа всех этих сил идет на приращение кинетической энергии частицы:

Согласно (5.8), работа сил поля равна убыли потенциальной энергии частицы, т. е. 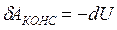. Подставив это выражение в предыдущее и перенеся член dU влево, получим

.

Отсюда видно, что работа сторонних сил идет на приращение величины

Т + U. Эту величину - сумму кинетической и потенциальной энергии частицы - называют ее полной механической энергией:

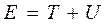. (5.22)

Заметим, что полная механическая энергия Е, как и потенциальная, определяется с точностью до прибавления несущественной произвольной постоянной.

Итак, приращение полной механической энергии частицы на элементарном перемещении равно

(5.23)

и на конечном перемещении из точки 1 в точку 2

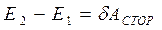. (5.24)

Последние две формулы выражают закон изменения полной механической энергии частицы: приращение полной механической энергии частицы на некотором пути равно алгебраической сумме работ всех сторонних сил, действующих на частицу на том же пути. Если , то полная механическая энергия частицы увеличивается, если же , то уменьшается.

Задача 5.3

С обрыва высотой h над поверхностью озера бросили камень массы m со скоростью v₀.. Найти работу, которую совершили силы сопротивления со стороны воздуха, если камень упал на воду со скоростью v. Согласно (5.24),

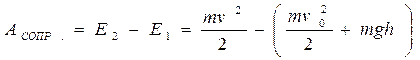
или

.

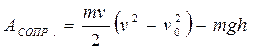Нетрудно сообразить, что эта работа должна быть величиной отрицательной (хотя, впрочем, при достаточно сильном ветре она может оказаться и положительной).

Закон изменения полной механической энергии частицы можно представить и в другой форме, поделив обе части (5.24) на соответствующий промежуток времени dt:

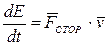(5.25)

Это значит, что производная полной механической энергии частицы по времени равна мощности результирующей всех сторонних сил, действующих на частицу.

Из закона изменения полной механической энергии частицы, в частности, следует закон сохранения этой величины. Если сторонние силы отсутствуют или таковы, что их суммарная мощность равна нулю за некоторый промежуток времени, то полная механическая энергия частицы остается постоянной в течение этого времени, т. е.

Е = Т + U = const,

или

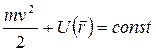. (5.26)

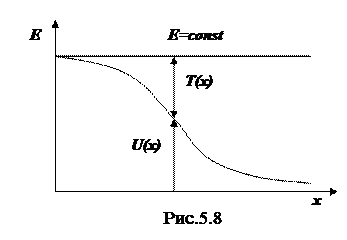Закон сохранения полной механической энергии частицы позволяет, например, не решая уравнений движения, определить скорость частицы в зависимости от ее положения (это сразу видно из последней формулы).

Соотношению (5.26) можно придать наглядный геометрический смысл. Пусть, например, частица движется вправо в потенциальном поле U(x), показанном на рис. 5.8. Если в точке х = 0 частица покоилась, то ее полная механическая энергия Е в этой точке равна потенциальной энергии. В отсутствие сторонних сил энергия Е частицы при движении будет оставаться постоянной (как показано на рисунке), а это значит, что по мере уменьшения ее потенциальной энергии будет расти кинетическая энергия. Зная же зависимость U(x), можно найти Т(х) и v(x), т. е. кинетическую энергию и скорость частицы в каждой точке.

В заключение рассмотрим пример, в котором роль закона сохранения как инструмента исследования проявляется особенно убедительно.

Задача 5.4

Шайба без трения скользит в горку высотой h, профиль которой зависит только от координаты X рис 5.9,а). Внизу шайба имеет скорость v₁, направление которой составляет угол α₁ с осью х (рис 5.9,б), где показан вид сверху. Найти направление движения шайбы после того, как она поднимется на горку, т. е. найти угол α₂.

Решение. Прежде всего отметим, что с помощью основного уравнения динамики эту задачу решить вообще невозможно, ибо не задан закон силы F, действующей на шайбу в области х₁ < х < х₂. Относительно этой силы известно только одно: она перпендикулярна оси Y.

Применим закон сохранения энергии:

,

откуда

(*)

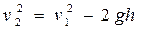Перепишем это выражение так:

Вследствие того, что сила поля перпендикулярна к оси Y, она не меняет v_у проекцию скорости; отсюда v_2y=v_ly. Поэтому предыдущее выражение упростится:

,

или

, (**)

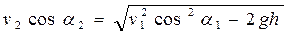где v₂ определяется уравнением (**). В результате

.

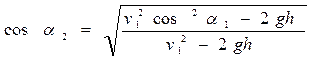Заметим, что приведенное решение справедливо, если подкоренное выражение в (••) не отрицательно, т. е. при 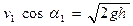. В противном случае шайба не преодолеет горку, т. е. произойдет ее «отражение» от потенциального барьера.

Дата добавления: 2014-11-29