Движение тела с переменной массой

Имеется много случаев, когда масса интересующего нас тела изменяется в процессе движения за счет непрерывного отделения или присоединения вещества (ракета, реактивный самолет, платформа, нагружаемая на ходу и др.).

Наша задача — найти закон движения такого тела. Рассмотрим решение этого вопроса для материальной точки, называя ее для краткости телом. Пусть в некоторый момент времени t масса движущегося тела А равна т, а присоединяемая (или отделяемая) масса имеет скорость относительно данного тела.

Введем вспомогательную инерциальную K - систему отсчета, скорость которой такова же, как и скорость тела А в данный момент времени t. Это значит, что в момент t тело А покоится в K - системе.

Пусть далее за промежуток времени от t до t + dt тело А приобретает в K - системе импульс 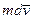. Этот импульс тело А получит, во-первых, вследствие присоединения (отделения) массы δт, которая приносит (уносит) импульс 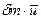, и, во-вторых, вследствие действия силы со стороны окружающих тел или силового поля. Таким образом, можно записать, что

,

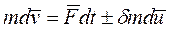где знак плюс соответствует присоединению массы, а знак минус — отделению.

Оба эти случая можно объединить, представив в виде приращения dm массы тела А (действительно, в случае присоединения массы 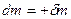, а в случае отделения 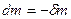. Тогда предыдущее уравнение примет вид

.

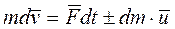Поделив это выражение на dt, получим

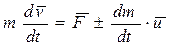, (6.8)

где 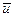- скорость присоединяемого (или отделяемого) вещества относительно рассматриваемого тела.

Это уравнение является основным уравнением динамики материальной точки с переменной массой. Его называют уравнением Мещерского. Будучи полученным в одной инерциальной системе отсчета, это уравнение в силу принципа относительности справедливо и в любой другой инерциальной системе. Заметим, что если система отсчета неинерциальна, то под силой следует понимать результирующую как сил взаимодействия данного тела с окружающими телами, так и сил инерции.

Последний член уравнения (6.8) носит название реактивной силы:

.

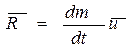Эта сила возникает в результате действия на данное тело присоединяемой (или отделяемой) массы. Если масса присоединяется то, 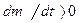, и вектор совпадает по направлению с вектором ; если же масса отделяется, то 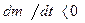, и вектор 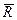противоположен вектору .

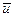Уравнение Мещерского по своей форме совпадает с основным уравнением динамики материальной точки постоянной массы: слева - произведение массы тела на ускорение, справа - действующие на него силы, включая реактивную силу. Однако в случае переменной массы мы не можем внести массу т под знак дифференцирования и представить левую часть уравнения как производную по времени от импульса, ибо

.

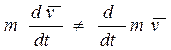Обратим внимание на два частных случая.

1. Если 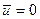, т. е. масса присоединяется или отделяется без скорости относительно тела, то 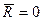и уравнение (6.8) принимает вид

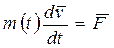, (6.9)

где m (t) - масса тела в данный момент времени.

Это уравнение определяет, например, движение платформы, из которой свободно высыпается песок. (см. Пример 6.4, пункт 1-й).

2. Если 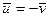, т. е. присоединяемая масса неподвижна в интересующей нас сиcтеме отсчета или отделяемая масса становится неподвижной в этой системе, то уравнение (6.8) принимает другой вид

,

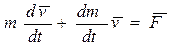или

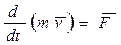. (6.10)

Иначе говоря, в этом частном случае - и только этом действие силы определяет изменение импульса тела с переменной массой. Данный случай реализуется, например, при движении платформы, нагружаемой сыпучим веществом из неподвижного бункера (см. Пример 6.4, пункт 2-й).

Задача 6.4.

Платформа в момент t = 0 начинает двигаться под действием постоянной силы тяги . Пренебрегая трением в осях, найти зависимость от времени скорости платформы, если:

1) она нагружена песком, который высыпается через отверстия в дне с постоянной скоростью μ (кг/с), а в момент t = 0 масса платформы с песком равна т₀;

2) на платформу, масса которой т₀, в момент t = 0 начинает высыпаться песок из неподвижного бункера так, что скорость погрузки постоянна и равна μ (кг/с).

Решение. 1. В этом случае реактивная сила равна нулю, и уравнение Мещерского (6.8) имеет вид

,

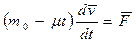Откуда

.

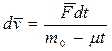Проинтегрировав это выражение с учетом начальных условий, получим

.

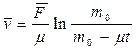2. В данном случае реактивная сила 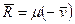, поэтому согласно уравнению (6.8)

.

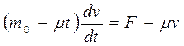Отсюда

.

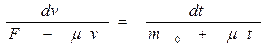Проинтегрировав это уравнение, получим

.

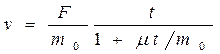Полученные в обоих случаях выражения справедливы, разумеется, лишь в процессе разгрузки (или погрузки) платформы.

Рассмотрим еще один пример на применение уравнения Мещерского.

Задача 6.5

Ракета движется в инерциальной К - системе отсчета в отсутствие внешнего силового поля, причем так, что газовая струя вылетает с постоянной относительно ракеты скоростью 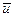. Найти зависимость скорости ракеты от ее массы т, если в момент старта ее масса была равна т₀.

В данном случае 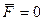и из уравнения (6.8) следует

.

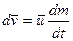Проинтегрировав это выражение с учетом начальных условий, получим

, (*)

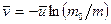где знак минус показывает, что вектор (скорость ракеты) противоположен по направлению вектору 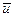. Отсюда, между прочим, видно, что скорость ракеты в данном случае ( 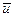= const) не зависит от времени сгорания топлива: определяется только отношением начальной массы ракеты т ₀ к оставшейся массе т.

Заметим, что если бы вся масса горючего была одновременно выброшена со скоростью 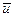относительно ракеты, то скорость последней оказалась бы иной. Действительно, если ракета вначале покоилась в интересующей нас инерциальной системе отсчета, а после одновременного выброса всего горючего приобрела скорость , то из закона сохранения импульса для системы ракета - горючее следует

,

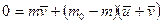где 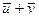- скорость горючего относительно данной системы отсчета. Отсюда

. (**)

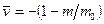Скорость ракеты в этом случае оказывается меньше, чем в предыдущем (при одинаковых значениях отношения т₀ / т). В этом нетрудно убедиться, сравнив характер зависимости от т₀ / т в обоих случаях. С ростом т₀ / т в первом случае (когда вещество отделяется непрерывно) скорость ракеты согласно (**) растет неограниченно, во втором же (когда вещество отделяется одновременно) скорость согласно (**) стремится к пределу, равному - .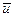

6.3 Центр инерции. Ц – система

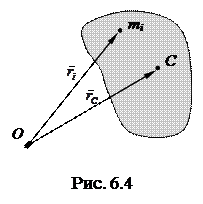Центр инерции. В любой системе частиц имеется одна замечательная точка С - центр инерции, или центр масс, - которая обладает рядом интересных и важных свойств. Ее положение относительно начала О данной системы отсчета характеризуется радиусом-вектором 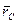, определяемым следующей формулой:

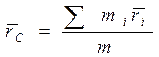(6.11)

где т _i и 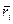- масса и радиус-вектор i -й частицы, т - масса всей системы (рис. 6.4).

Следует заметить, что центр инерции системы совпадает с ее центром тяжести. Правда, это утверждение справедливо лишь в том случае, когда поле сил тяжести в пределах данной системы можно считать однородным.

Найдем теперь скорость центра инерции в данной системе отсчета. Продифференцировав (6.11) по времени, получим

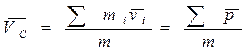(6.12)

Если скорость центра инерции равна нулю, то говорят, что система как целое покоится. Это вполне естественное обобщение понятия покоя отдельной частицы. Скорость же 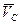приобретает смысл скорости движения системы как целого.

Запишем (6.12) в виде

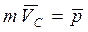, (6.13)

где 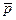- полный импульс системы.

Продифференцировав это выражение по времени и учтя (6.4), получим уравнение движения центра инерции:

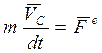(6.14)

где 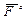- результирующая всех внешних сил.

Таким образом, если на систему действуют внешние силы (и она в общем случае совершает любое сложное движение), одна ее точка - центр инерции - движется так, как если бы все внешние силы были приложены к этой точке, и масса всей системы была бы сосредоточена в этой точке. При этом важно заметить, что движение центра инерции совершенно не зависит от точек приложения данных внешних сил.

Далее, если 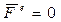, то центр инерции системы покоится или движется равномерно и прямолинейно. Так ведет себя центр инерции, например, замкнутой системы.

Уравнение (6.14) по форме совпадает с основным уравнением динамики материальной точки и является его естественным обобщением на систему частиц: ускорение системы как целого прямо пропорционально результирующей всех внешних сил и обратно пропорционально суммарной массе системы. Напомним, что в неинерциальных системах отсчета результирующая всех внешних сил включает в себя как силы взаимодействия с окружающими телами, так и силы инерции.

Рассмотрим три примера на движение центра инерции системы.

Задача 6.6

Покажем, как можно иначе решить задачу с человеком на плоту (см. пример 6.3), воспользовавшись поведением центра инерции этой системы.

Так как сопротивление воды пренебрежимо мало, то результирующая всех внешних сил, действующих на систему человек - плот, равна нулю. А это значит, что положение центра инерции данной системы в процессе движения человека (и плота) меняться не будет, т. е.

,

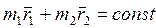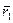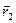где и - радиус-векторы, характеризующие положения центров инерции человека и плота относительно некоторой точки воды. Из этого равенства найдем связь между приращениями векторов 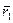и :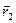

.

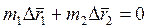Имея в виду, что приращения 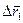и 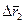представляют собой перемещения человека и плота относительно воды, причем , найдем перемещение плота:

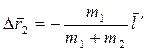
Задача 6.7

Человек прыгает с вышки в воду. Движение прыгуна в общем случае имеет весьма сложный характер. Однако если сопротивление воздуха пренебрежимо мало, то можно сразу утверждать, что центр инерции прыгуна движется по параболе, как материальная точка, на которую действует постоянная сила 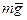, где т - масса человека.

Задача 6.8

Замкнутая цепочка, соединенная нитью с концом оси центробежной машины, равномерно вращается вокруг вертикальной оси с угловой скоростью ω (рис. 6.5). При этом нить образует угол ξ с вертикалью. Как ведет себя центр инерции цепочки?

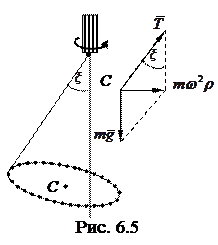Прежде всего ясно, что при равномерном вращении центр инерции цепочки не движется в вертикальном направлении. Это значит, что вертикальная составляющая силы натяжения нити компенсирует силу тяжести (см. рис. 6.5справа). Горизонтальная же составляющая силы натяжения постоянна по модулю и все время направлена к оси вращения. Отсюда следует, что центр инерции цепочки - точка С – движется по горизонтальной окружности радиус которой ρ легко найти с помощью формулы (6.14), записав ее в виде

,

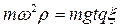где т - масса цепочки. При этом точка С все время находится между осью вращения и нитью, как показано на рис. 6.5

Ц - система. В тех часто встречающихся случаях, когда нас интересует лишь относительное движение частиц внутри системы и не интересует движение этой системы как целого, наиболее целесообразно пользоваться системой отсчета, в которой центр инерции покоится. Это позволяет значительно упростить и анализ явления, и соответствующие расчеты.

Систему отсчета, жестко связанную с центром инерции данной системы частиц и перемещающуюся поступательно по отношению к инерциальным системам, называют системой центра инерции, или, кратко, Ц - системой. Отличительной особенностью Ц - системы является то, что полный импульс системы частиц в ней равен нулю - это непосредственно следует из формулы (6.13). Другими словами, любая система частиц как целое покоится в своей Ц - системе.

Для замкнутой системы частиц ее Ц - система является инерциальной, для незамкнутой - в общем случае неинерциальной.

Найдем связь между значениями механической энергии системы в K - и Ц - системах отсчета. Начнем с кинетической энергии системы Т. Скорость i - й частицы в K - системе можно представить как

,

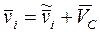где - скорость этой частицы в Ц - системе, а 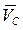- скорость Ц - системы относительно K - системы отсчета.

Тогда можно записать:

.

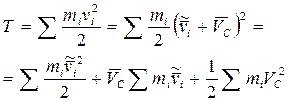Так как в Ц – системе 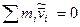, то предыдущее выражение примет вид

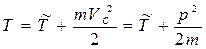, (6.15)

где 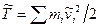- суммарная кинетическая энергия частиц в Ц - системе, m - масса всей системы, р — ее полный импульс в К - системе отсчета.

Таким образом, кинетическая энергия системы частиц складывается из суммарной кинетической энергии Т в Ц - системе и кинетической энергии, связанной с движением системы частиц как целого. Это важный вывод, и он неоднократно будет использоваться в дальнейшем (в частности, при изучении динамики твердого тела).

Из формулы (6.15) следует, что кинетическая энергия системы частиц минимальна в Ц – системе - в этом еще одна особенность Ц - системы. Действительно, в Ц - системе 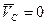и поэтому в (6.15) остается только Т.

Теперь перейдем к полной механической энергии Е. Так как собственная потенциальная энергия системы U зависит только от конфигурации системы, то значение U одинаково во всех системах отсчета. Добавив U слева и справа равенства (6.15), получим формулу преобразования полной механической энергии при переходе от K - к Ц - системе:

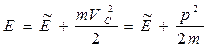. (6.16)

Энергию

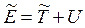
часто называют внутренней механической энергией системы.

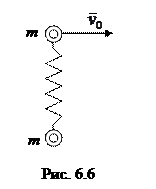Задача 6.9

На гладкой горизонтальной плоскости лежат две небольшие шайбы, каждая массы т, которые соединены между собой невесомой пружинкой. Одной из шайб сообщили начальную скорость v ₀, как показано на рис. 6.6

Какова внутренняя механическая энергия 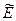этой системы в процессе движения?

Поскольку плоскость гладкая, система в процессе движения будет вести себя как замкнутая. Поэтому ее полная механическая энергия Е и суммарный импульс 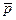будут сохраняться, оставаясь равными тем значениям, которые они получили в начальный момент, т. е. 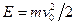, 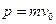. Подставив эти значения в формулу (6.16), получим

.

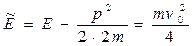Нетрудно сообразить, что внутренняя энергия 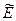связана с вращением и колебанием данной системы, причем в начальный момент 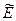была равна только энергии вращательного движения.

Если система частиц замкнута и в ней происходят процессы, связанные с изменением полной механической энергии, то из (6.16) следует, что 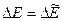, т. е. приращение полной механической энергии относительно произвольной инерциальной системы отсчета равно приращению внутренней механической энергии. При этом кинетическая энергия, обусловленная движением системы частиц как целого, не меняется, ибо для замкнутой системы 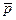= const.

В частности, если замкнутая система консервативна, то ее полная механическая энергия сохраняется во всех инерциальных системах отсчета. Этот вывод находится в полном соответствии с принципом относительности Галилея.

Система из двух частиц. Пусть массы частиц равны т ₁ и т ₂, а их скорости в K - системе отсчета 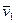и 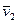соответственно. Найдем выражения, определяющие их импульсы и суммарную кинетическую энергию в Ц - системе.

Импульс первой частицы в Ц – системе

,

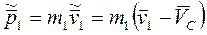где 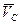скорость центра инерции (Ц – системы) в K - системе отсчета.

После подстановки в эту формулу выражения (6.12) для 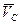получим

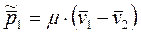, (6.17)

где μ - так называемая приведенная масса системы,

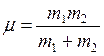. (6.18)

Аналогично импульс второй частицы в Ц – системе

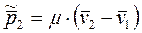(6.19)

Таким образом, импульсы обеих частиц в Ц - системе одинаковы по модулю и противоположны по направлению, причем модуль импульса каждой частицы

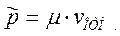, (6.20)

где 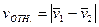- скорость одной частицы относительно другой.

Теперь обратимся к кинетической энергии. Суммарная кинетическая энергия обеих частиц в Ц – системе

.

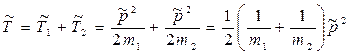Так как согласно (4.18) 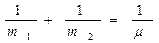, то

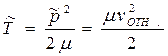. (6.21)

Если частицы взаимодействуют друг с другом, то полная механическая энергия обеих частиц в Ц – системе

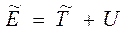(6.22)

где U - потенциальная энергия взаимодействия данных частиц.

Полученные формулы играют большую роль при изучении столкновения частиц.

Дата добавления: 2014-11-29