Момент импульса частицы. Момент силы

Анализ поведения систем показывает, что кроме энергии и импульса существует еще одна механическая величина, с которой также связан закон сохранения, - это так называемый момент импульса *. Что это за величина и каковы ее свойства?

__________________

* Употребляются также названия вращательный момент, угловой момент или просто момент. Прежнее название — момент количества движения.

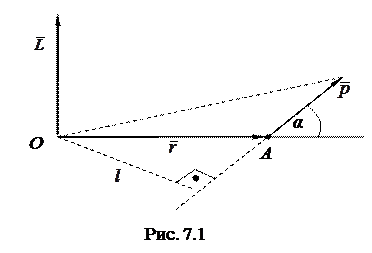Сначала рассмотрим одну частицу. Пусть 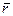- радиус-вектор, характеризующий ее положение относительно некоторой точки О выбранной системы отсчета, а 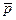- ее импульс в этой системе. Моментом импульса частицы А относительно точки О (рис. 7.1) называют вектор , равный векторному произведению вектора 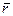на вектор :

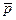. (7.1)

Из этого определения следует, что является аксиальным вектором. Его направление выбрано так, что вращение вокруг точки О в направлении вектора 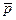и вектор образуют правовинтовую систему. Модуль вектора равен:

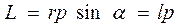, (7.2)

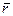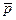где α - угол между векторами и , а 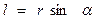- плечо вектора 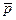относительно точки О (см. рис. 7.1).

Выясним, какая механическая величина ответственна за изменение вектора в данной системе отсчета. Для этого продифференцируем (7.1) по времени:

.

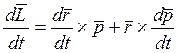Так как точка О неподвижна, то вектор 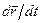равен скорости частицы, т. е. совпадает по направлению с вектором 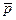, и поэтому

.

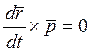Далее, согласно второму закону Ньютона, 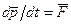, где - равнодействующая всех сил, приложенных к частице. Следовательно,

.

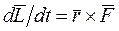Величину, стоящую в правой части этого уравнения, называют моментом силы относительно точки О (рис. 7.2). Обозначив ее буквой , запишем

. (7.3)

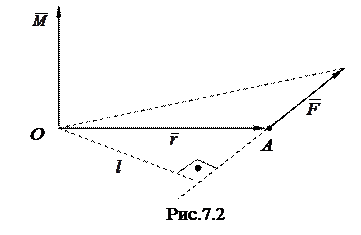Вектор , как и , является аксиальным. Модуль этого вектора, аналогично (7.2), равен

М = l F, (7.4)

где l — плечо вектора относительно точки О (см. рис. 7.2).

Итак, производная по времени от момента импульса частицы относительно некоторой точки О выбранной системы отсчета равна моменту равнодействующей силы относительно той же точки О:

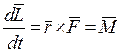. (7.5)

Это уравнение называют уравнением моментов. Заметим, что если система отсчета является неинерциальной, то момент силы включает в себя как момент сил взаимодействия, так и момент сил инерции (относительно той же точки О).

Из уравнения моментов (7.5), в частности, следует, что если 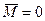, то 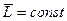. Другими словами, если относительно некоторой точки О выбранной системы отсчета момент всех сил, действующих на частицу, равен нулю в течение интересующего нас промежутка времени, то относительно этой точки момент импульса частицы остается постоянным в течение этого времени.

Задача 7.1

Некоторая планета А движется в поле тяготения Солнца С (рис. 7.3). Относительно, какой точки гелиоцентрической системы отсчета момент импульса данной планеты будет сохраняться во времени? Для ответа на этот вопрос, прежде всего, необходимо установить, какие силы действуют на планету А. В данном случае это только сила тяготения F со стороны Солнца. Так как при движении планеты направление этой силы все время проходит через центр Солнца, то последний и является той точкой, относительно которой момент силы все время равен нулю и момент импульса планеты будет оставаться постоянным. Импульс же 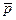планеты при этом будет меняться.

Задача 7.2

Шайба А, двигаясь по гладкой горизонтальной плоскости, упруго отскакивает от гладкой вертикальной стенки (рис. 7.4, вид сверху). Найти точку, относительно которой момент импульса шайбы будет оставаться постоянным в этом процессе.

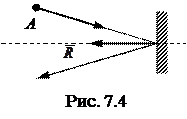На шайбу действуют сила тяжести, сила реакции со стороны горизонтальной плоскости и в момент удара о вертикальную стенку - сила реакции 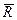со стороны этой стенки. Первые две силы уравновешивают друг друга, остается сила 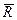. Ее момент равен нулю относительно любой точки, лежащей на линии действия вектора 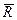, а значит, относительно любой из этих точек момент импульса шайбы будет оставаться постоянным в данном процессе.

Задача 7.3

На горизонтальной гладкой плоскости находятся неподвижный вертикальный цилиндр и шайба А, соединенная с цилиндром нитью АВ (рис. 7.5, вид сверху). Шайбе сообщили начальную скорость , как показано на этом рисунке. Есть ли здесь точка, относительно которой момент импульса шайбы будет оставаться постоянным в процессе движения?

В данном случае единственная некомпенсированная сила, действующая на шайбу А,- это сила натяжения со стороны нити. Нетрудно видеть, что точки, относительно которой момент силы в процессе движения был бы все время равен нулю, здесь нет. А следовательно, нет и точки, относительно которой момент импульса шайбы оставался бы постоянным. Этот пример показывает, что не всегда существует точка, относительно которой момент импульса частицы оставался бы постоянным.

Уравнение (7.5) позволяет получить ответ на два типичных вопроса:

1) найти момент силы относительно интересующей нас точки О в любой момент времени t, если известна зависимость от времени момента импульса частицы 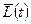относительно той же точки;

2) определить приращение момента импульса частицы относительно точки О за любой промежуток времени, если известна зависимость от времени момента силы , действующего на эту частицу (относительно той же точки О).

Решение первого вопроса сводится к нахождению производной по времени от момента импульса, т. е. 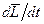, которая и равна согласно (5.5) искомому моменту силы .

Решение же второго вопроса сводится к интегрированию уравнения (5.5). Умножив обе части этого уравнения на dt, получим 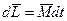- выражение, которое определяет элементарное приращение вектора . Проинтегрировав это выражение по времени, найдем приращение вектора за конечный промежуток времени t:

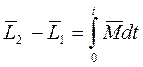. (7.6)

Величину, стоящую в правой части этого равенства, называют импульсом момента силы. Таким образом, приращение момента импульса частицы за любой промежуток времени равно импульсу момента силы за это же время.

Рассмотрим два примера.

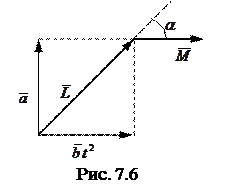Задача 7.4

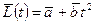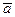Момент импульса частицы относительно некоторой точки меняется со временем t по закону , где и 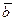- некоторые постоянные векторы, причем 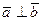. Найти момент силы , действующий на частицу, когда угол между векторами и окажется равным 45°.

Решение. Согласно (7.5),

,

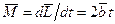т. е. вектор все время совпадает по направлению с вектором 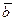. Изобразим векторы и в некоторый момент t (рис. 7.6). Из этого рисунка видно, что угол α = 45° в момент t₀, когда .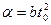

Отсюда 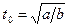и .

Задача 7.5

Камень А массы т. бросили под углом к горизонту с начальной скоростью 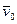. пренебрегая сопротивлением воздуха, найти зависимость от времени момента импульса камня 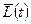относительно точки бросания О (рис. 7.7).

Решение. За промежуток времени dt момент импульса камня относительно точки О получит приращение

.

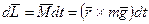Так как 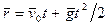, то 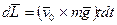. Проинтегрировав это выражение с учетом того, что в момент t =0 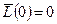, получим 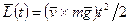. Отсюда видно, что направление вектора остается неизменным в процессе движения (вектор направлен за плоскость рис. 7.7).

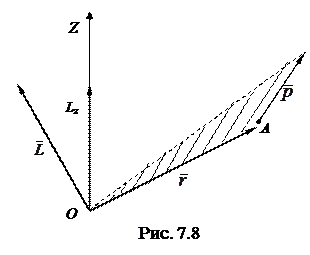
Момент импульса и момент силы относительно оси. Возьмем в интересующей нас системе отсчета произвольную неподвижную ось Z. Пусть относительно некоторой точки О на оси Z момент импульса частицы А равен , а момент силы, действующий на частицу, - .

Моментом импульса относительно оси Z называют проекцию на эту ось вектора , определенного относительно произвольной точки О данной оси (рис. 7.8). Аналогично вводят и понятие момента силы относительно оси. Их обозначают соответственно L_z и М_z. Далее мы увидим, что так определенные L_z и М_z не зависят от выбора точки О на оси Z.

Выясним свойства этих величин. Спроектировав (7.5) на ось Z, получим

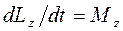, (7.7)

т. е. производная по времени от момента импульса частицы относительно оси Z равна моменту силы относительно этой оси. В частности, если M_z = 0, то

L_z = const. Другими словами, если момент силы относительно некоторой неподвижной оси Z равен нулю, то момент импульса частицы относительно этой оси остается постоянным. При этом сам вектор может и меняться.

Рассмотрим в качестве примера случай, когда небольшое тело массы т, подвешенное на нити, равномерно движется по горизонтальной окружности (рис. 7.9). Относительно точки О момент импульса тела - вектор - находится в одной плоскости с осью Z и нитью, и при движении тела вектор под действием момента силы тяжести все время поворачивается, т. е. меняется. Проекция же L_z остается при этом постоянной, так как вектор перпендикулярен к оси Z и M_z = 0,

Найдем теперь аналитические выражения для L_z и M_z. Нетрудно видеть, что эта задача сводится к нахождению проекций на ось Z векторных произведений и .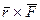

Воспользуемся цилиндрической системой координат ρ, φ, Z, связав с частицей А (рис. 7.10) орты 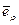, , 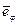, 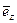которые направлены в сторону возрастания соответствующих координат. В этой системе координат радиус-вектор 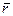и импульс 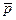частицы записывают так:

,

,

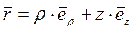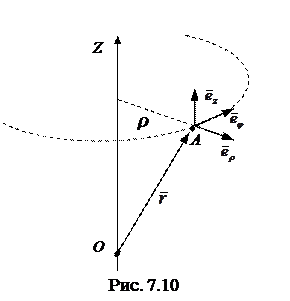
где р_ρ, р_φ, р_z - проекции вектора 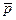на соответствующие орты.

Из векторной алгебры известно, что векторное произведение можно представить определителем

.

Отсюда сразу видно, что

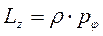, (7.8)

где ρ - расстояние частицы от оси Z, р_φ - проекция вектора 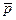на орт .

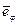Преобразуем это выражение к другому виду, наиболее удобному для практических применений. Имея в виду, что р_φ = mv_φ = тρ , получим

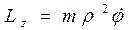. (7.9)

Аналогично (7.8) записывается и М_z - момент силы относительно оси Z.

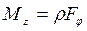(7.10)

где F_φ - проекция вектора силы F на орт .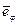

Обратим внимание, что L_z и М_z действительно не зависят от выбора точки О на оси Z, относительно которой определены векторы и . Кроме того, видно, что L_z и М_z - величины алгебраические, их знаки соответствуют знакам проекций р_φ и F_φ.

Дата добавления: 2014-11-29