
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон сохранения момента импульса системы
|
|
|
|
Рассмотрим произвольную систему частиц. Введем понятие момента импульса данной системы как векторную сумму моментов импульсов ее отдельных частиц:
 , (7.11)
, (7.11)
где все векторы определены относительно одной и той же точки О интересующей нас системы отсчета. Заметим, что момент импульса системы - величина аддитивная: момент импульса системы равен сумме моментов импульсов ее отдельных частей независимо от того, взаимодействуют они между собой или нет.
Выясним, какая величина определяет изменение момента импульса системы. Для этого продифференцируем (7.11) по времени: 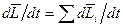 . В предыдущем параграфе было показано, что производная
. В предыдущем параграфе было показано, что производная 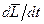 равна моменту всех сил, действующих на k -ю частицу. Представим этот момент в виде суммы
равна моменту всех сил, действующих на k -ю частицу. Представим этот момент в виде суммы 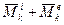 , где
, где  , и
, и  ; — результирующие моменты внутренних и внешних сил, действующих на данную частицу. Тогда
; — результирующие моменты внутренних и внешних сил, действующих на данную частицу. Тогда
 .
.
Здесь первая сумма - это суммарный момент всех внутренних сил относительно точки О, вторая сумма - суммарный момент всех внешних сил относительно той же точки О.
Покажем, что суммарный момент всех внутренних сил относительно любой точки равен нулю. Действительно, внутренние силы — это силы взаимодействия между частицами данной системы. По третьему закону Ньютона, эти силы попарно одинаковы по модулю, противоположны по направлению и лежат на одной прямой, т. е. имеют одинаковое плечо. Поэтому моменты сил каждой пары взаимодействия равны по модулю и противоположны по направлению, т. е. уравновешивают друг друга, и, значит, суммарный момент всех внутренних сил всегда равен нулю.
В результате последнее уравнение принимает вид
 . (7.12)
. (7.12)
Это означает, что производная по времени от момента импульса системы равна суммарному моменту  всех внешних сил. Разумеется, оба момента,
всех внешних сил. Разумеется, оба момента,  и
и  , здесь определены относительно одной и той же точки О интересующей нас системы отсчета. Последнее уравнение выражает закон изменения момента импульса системы.
, здесь определены относительно одной и той же точки О интересующей нас системы отсчета. Последнее уравнение выражает закон изменения момента импульса системы.
Заметим, что уравнение (7.12) справедливо в любой системе отсчета, как инерциальной, так и неинерциальной. Необходимо только помнить, что в неинерциальной системе отсчета нужно учитывать и действие сил инерции, играющих роль внешних сил, т. е. под  в (7.12) следует понимать сумму
в (7.12) следует понимать сумму  , где
, где  - суммарный момент внешних сил взаимодействия, а
- суммарный момент внешних сил взаимодействия, а  - суммарный момент сил инерции (относительно одной и той же точки О системы отсчета).
- суммарный момент сил инерции (относительно одной и той же точки О системы отсчета).
Как и в случае одной частицы, из формулы (7.12) следует, что приращение момента импульса системы за конечный промежуток времени t есть
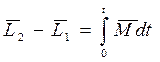 , (7.13)
, (7.13)
приращение момента импульса системы равно импульсу суммарного момента всех внешних сил. И здесь, конечно, оба момента  и
и  , определены относительно одной и той же точки О выбранной системы отсчета.
, определены относительно одной и той же точки О выбранной системы отсчета.
Итак, мы пришли к важному выводу: момент импульса  системы может изменяться под действием только момента
системы может изменяться под действием только момента  всех внешних сил. Внутренние силы не могут изменить момента импульса системы. Отсюда непосредственно вытекает другой важный вывод - закон сохранения момента импульса замкнутой системы: момент импульса
всех внешних сил. Внутренние силы не могут изменить момента импульса системы. Отсюда непосредственно вытекает другой важный вывод - закон сохранения момента импульса замкнутой системы: момент импульса  замкнутой системы остается постоянным относительно любой точки произвольной инерциальной системы отсчета. Действительно, в случае замкнутой системы внешние силы отсутствуют, а значит, их момент
замкнутой системы остается постоянным относительно любой точки произвольной инерциальной системы отсчета. Действительно, в случае замкнутой системы внешние силы отсутствуют, а значит, их момент  =0, и согласно (7.12)
=0, и согласно (7.12)
 . (7.14)
. (7.14)
Так, например, ведет себя момент импульса Солнечной системы, которая является практически замкнутой.
Сохранение во времени момента импульса  замкнутой системы отнюдь не означает сохранение моментов импульсов ее отдельных частей. Моменты импульса последних могут изменяться во времени под действием внутренних сил, что и подчеркнуто в (7.14). Однако эти изменения происходят так, что приращение момента импульса одной части замкнутой системы в точности равно убыли момента импульса ее другой части.
замкнутой системы отнюдь не означает сохранение моментов импульсов ее отдельных частей. Моменты импульса последних могут изменяться во времени под действием внутренних сил, что и подчеркнуто в (7.14). Однако эти изменения происходят так, что приращение момента импульса одной части замкнутой системы в точности равно убыли момента импульса ее другой части.
Закон сохранения момента импульса играет такую же важную роль, как и законы сохранения энергии и импульса. Уже сам по себе он позволяет сделать во многих случаях ряд существенных заключений о свойствах тех или иных процессов, совершенно не вникая в их детальное рассмотрение. Иллюстрацией этому может служить такой пример.
Задача 7.6
Два одинаковых шара насажены на гладкий горизонтальный стержень, по которому они могут скользить (рис. 7.11). Шары сближают и соединяют нитью. Затем всю установку приводят во вращение вокруг вертикальной оси, предоставляют ее самой себе и пережигают нить. Шары, естественно, разлетаются к концам стержня. Угловая же скорость установки при этом резко уменьшается.
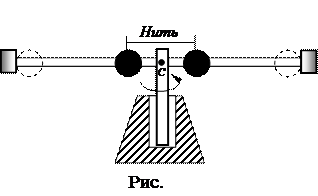 Наблюдаемый эффект является прямым следствием закона сохранения момента импульса, ибо данная установка ведет себя по существу как замкнутая (внешние силы компенсируют друг друга, силы трения в оси малы). Для количественной оценки изменения угловой скорости будем считать, что масса всей установки практически сосредоточена в шарах, а их размеры пренебрежимо малы. Тогда из равенства момента импульса шаров относительно точки С в начальном и конечном состояниях системы:
Наблюдаемый эффект является прямым следствием закона сохранения момента импульса, ибо данная установка ведет себя по существу как замкнутая (внешние силы компенсируют друг друга, силы трения в оси малы). Для количественной оценки изменения угловой скорости будем считать, что масса всей установки практически сосредоточена в шарах, а их размеры пренебрежимо малы. Тогда из равенства момента импульса шаров относительно точки С в начальном и конечном состояниях системы: 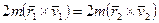 , - следует
, - следует
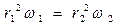
Отсюда видно, что с увеличением расстояния r шаров от оси вращения угловая скорость установки уменьшается (как 1 / r2). И наоборот, если бы расстояние между шарами уменьшалось (под действием каких-либо внутренних сил), угловая скорость установки увеличивалась бы. Этот эффект имеет общий характер, и его широко используют, например, фигуристы и гимнасты.
Обратим внимание на тот факт, что конечный результат совершенно не зависит от характера внутренних сил (здесь — это силы трения между шарами и стержнем).
Особый интерес представляют случаи, когда момент импульса  сохраняется для незамкнутых систем, у которых, как известно, импульс
сохраняется для незамкнутых систем, у которых, как известно, импульс 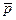 меняется со временем. Если относительно некоторой точки О выбранной системы отсчета суммарный момент внешних сил
меняется со временем. Если относительно некоторой точки О выбранной системы отсчета суммарный момент внешних сил  = 0 в течение интересующего нас промежутка времени, то согласно (7.12) момент импульса системы относительно точки О сохраняется за это время. В случае незамкнутых систем такой точки, может и не быть, что следует, прежде всего, выяснить для каждого конкретного случая.
= 0 в течение интересующего нас промежутка времени, то согласно (7.12) момент импульса системы относительно точки О сохраняется за это время. В случае незамкнутых систем такой точки, может и не быть, что следует, прежде всего, выяснить для каждого конкретного случая.
Задача 7.7
Система Земля - Луна, движущаяся в поле тяготения Солнца, является незамкнутой. Ее импульс все время меняется под действием сил тяготения. Здесь, однако, имеется одна точка, относительно которой момент сил тяготения, действующий на данную систему, все время равен нулю - это центр Солнца. Поэтому можно сразу утверждать, что момент импульса системы Земля - Луна относительно центра Солнца остается постоянным.
 Задача 7.8
Задача 7.8
На гладкой горизонтальной плоскости лежит стержень ОВ, который может свободно вращаться вокруг неподвижной вертикальной оси, проходящей через его конец О (рис. 7.12). В конец В стержня попадает, застревая, шайба А, скользившая по плоскости, и далее вся система начинает вращаться, как единое целое вокруг точки О.
Ясно, что система шайба - стержень незамкнутая: кроме сил, уравновешивающих друг друга в вертикальном направлении, со стороны оси в процессе удара будет действовать горизонтальная сила, а после того, как стержень начнет вращаться, возникает еще одна сила со стороны оси, благодаря которой центр инерции системы будет двигаться по окружности. Но обе силы проходят через точку О, а следовательно, момент этих внешних сил относительно точки О все время равен нулю. Отсюда вывод: момент импульса данной системы будет оставаться постоянным относительно точки О.
В более ограниченном виде закон сохранения момента импульса выполняется в тех случаях, когда проекция момента внешних сил на некоторую неподвижную ось Z равна нулю. В самом деле, спроектировав (7.12) на ось Z получим
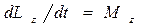 . (7.15)
. (7.15)
Здесь Lz и Мz - момент импульса системы и суммарный момент внешних сил относительно оси Z:

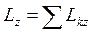 ,
,  , (7.16)
, (7.16)
где 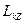 и
и  — момент импульса и момент внешних сил относительно оси Z для k - й частицы системы.
— момент импульса и момент внешних сил относительно оси Z для k - й частицы системы.
Уравнение (7.15) выражает закон изменения момента импульса системы относительно оси. Из него следует, что если относительно некоторой неподвижной в данной системе отсчета оси Z Мz = 0, то момент импульса системы относительно этой оси сохраняется:
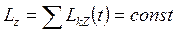 . (7.17)
. (7.17)
При этом сам вектор  , определенный относительно произвольной точки О на этой оси, может меняться. Например, если система движется в однородном поле тяжести, то суммарный момент всех сил тяжести относительно любой неподвижной точки О перпендикулярен к вертикали, а значит, относительно любой вертикальной оси Мz = О и Lz = const, чего нельзя сказать о векторе
, определенный относительно произвольной точки О на этой оси, может меняться. Например, если система движется в однородном поле тяжести, то суммарный момент всех сил тяжести относительно любой неподвижной точки О перпендикулярен к вертикали, а значит, относительно любой вертикальной оси Мz = О и Lz = const, чего нельзя сказать о векторе  .
.
В заключение необходимо затронуть вопрос об универсальности закона сохранения момента импульса. Можно было заметить, что рассуждения, которые нас привели к закону сохранения этой величины, целиком опирались на справедливость законов Ньютона.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1211; Нарушение авторских прав?; Мы поможем в написании вашей работы!