Законы изменения и сохранения импульса

Импульс частицы. Импульс^* частицы по определению, есть

,

где т - масса частицы, 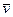- ее скорость в рассматриваемой системе отсчета.

Выясним, какая физическая величина ответственна за изменение импульса частицы. Для этого продифференцируем 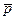по времени. Так как в классической механике масса частицы как таковой есть величина постоянная, то . Согласно второму закону Ньютона, правая часть этого выражения равна результирующей силе , действующей на частицу, поэтому

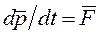. (6.1)

Это уравнение представляет собой другую форму записи второго закона Ньютона; оно означает, что производная по времени от импульса частицы равна действующей силе. В частности, если 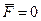, то .

Из уравнения (6.1) следует также, что, зная , можно определить и силу , действующую на частицу.

Заметим, что в неинерциальной системе отсчета сила включает в себя не только силы взаимодействия данной частицы с другими телами, но и силы инерции.

Уравнение (6.1) позволяет найти приращение импульса частицы за любой промежуток времени, если известна зависимость силы от времени.

Действительно, из (6.1) следует, что элементарное приращение импульса частицы за промежуток времени dt есть 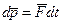. Проинтегрировав это выражение по времени, найдем приращение импульса частицы за конечный промежуток времени t:

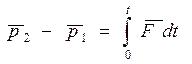. (6.2)

Величину, стоящую в правой части этого равенства, называют импульсом силы. Таким образом, приращение импульса частицы за любой промежуток времени равно импульсу силы за то же время. Если сила , то вектор можно вынести из-под интеграла и тогда .

____________________

* Прежнее название этой величины — количество движения.

Пока речь идет об одной частице, понятие импульса ничего принципиально нового не вносит. Иначе обстоит дело при переходе к системе частиц.

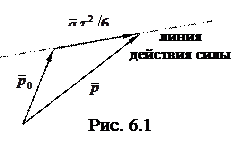Задача 6.1

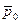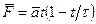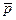На частицу, которая в начальный момент t = 0 имела импульс , действует в течение промежутка времени τ сила , где . Найти импульс частицы после окончания действия этой силы.

Решение. Согласно (6.2),

.

Вычислив интеграл, получим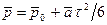

(рис. 6.1).

Импульс системы. Рассмотрим произвольную систему частиц. Введем понятие импульса системы как векторную сумму импульсов ее отдельных

частиц:

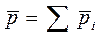. (6.3)

где 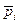- импульс i - й частицы.

Заметим, что импульс системы - величина аддитивная, т. е. импульс системы равен сумме импульсов ее отдельных частей независимо от того, взаимодействуют они между собой или нет.

Найдем физическую величину, которая определяет изменение импульса системы. Для этого продифференцируем (6.3) по времени:

.

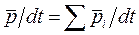Согласно (6.1)

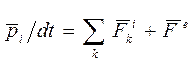
где - силы, действующие на k - ю частицу со стороны других частиц системы (внутренние силы); 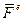- сила, действующая на эту же частицу со стороны других тел, не входящих в рассматриваемую систему (внешние силы).

После подстановки последнего выражения в предыдущее получим

.

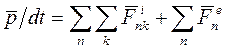Двойная сумма справа - это сумма всех внутренних сил. В соответствии с третьим законом Ньютона силы взаимодействия между частицами системы попарно одинаковы по величине и противоположны по направлению. Поэтому сумма всех внутренних сил равна нулю. В результате

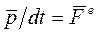, 6.4)

где 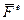- результирующая всех внешних сил, .

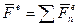Формула (6.4) выражает закон изменения импульса системы: производная по времени от импульса системы равна векторной сумме всех внешних сил, действующих на частицы системы.

В неинерциальной системе отсчета результирующая всех внешних сил включает в себя не только силы взаимодействия с другими телами, но и силы инерции.

Как и в случае одной частицы, из формулы (6.4) следует, что приращение импульса системы за конечный промежуток времени t есть

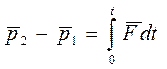(6.5)

т. е. приращение импульса системы равно импульсу результирующей всех внешних сил за тот же промежуток времени.

Итак, импульс системы могут изменить только внешние силы. В частности, если результирующая всех внешних сил 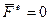, то импульс системы

(6.6)

Это уравнение выражает закон сохранения импульса системы: импульс системы остается постоянным, если результирующая всех внешних сил равна нулю (в течение интересующего нас промежутка времени).

Отсюда, в частности, следует, что импульс замкнутой системы есть величина постоянная. При этом импульсы отдельных частиц (частей) системы могут меняться во времени (что и подчеркнуто в последнем уравнении), однако эти изменения происходят так, что приращение импульса одной части системы в точности равно его убыли в другой части системы.

Задача 6.2

Орудие массы т соскальзывает по гладкой наклонной плоскости, составляющей угол α с горизонтом. В момент, когда скорость орудия равна , производят выстрел, в результате которого орудие остановилось, а вылетевший в горизонтальном направлении снаряд «унес» импульс 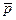. Пусть продолжительность выстрела равна τ. Каково среднее за время τ значение силы реакции 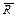со стороны наклонной плоскости? Здесь система орудие - снаряд незамкнутая. За время τ эта система получает приращение импульса, равное . Изменение импульса системы обусловлено действием двух внешних сил: силы реакции 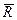(ось X перпендикулярна к наклонной плоскости) и силы тяжести 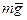. Поэтому можно написать: ,

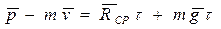где 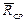- среднее за время τ значение вектора . Это соотношение очень полезно представить графически (рис.6.2). Из рисунка сразу видно, что искомое значение 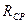определяется формулой

.

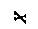
Задача 6.3

На поверхности воды покоится узкий длинный плот массы т ₁ с человеком массы т ₂. Начав двигаться, человек совершил перемещение 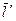относительно плота и затем остановился. Сопротивление воды пренебрежимо мало. Найдем перемещение 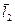, которое совершил при этом плот относительно воды.

В данном случае результирующая всех внешних сил, действующих на систему человек - плот, равна нулю, а поэтому импульс этой системы меняться не будет, оставаясь равным нулю в процессе движения:

,

где 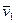и 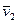- скорости плота и человека относительно воды.

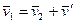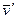Но скорость человека относительно воды можно представить в виде , где - скорость человека относительно плота. Исключив 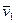из этих двух уравнений, получим

Умножив обе части на dt, найдем связь между элементарными перемещениями плота d 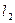и человека 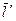относительно плота. Такая же связь будет, очевидно, и для конечных перемещений:

.

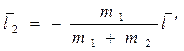Отсюда видно, что перемещение плота 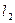не зависит от характера движения человека, т. е. не зависит от закона .

Вернемся к закону сохранения импульса. Хотя этот закон справедлив при условии, что результирующая всех внешних сил 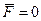, в более ограниченном виде он может иметь место и для некоторых случаев, когда . А именно: если проекция результирующей внешней силы на некоторое направление X равна нулю, то проекция импульса системы на это направление сохраняется. Действительно, проектируя (6.4) на направление X, получим

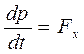, (6.7)

откуда следует, что если F_x = 0, то р_х = const, Например, при движении системы в однородном поле сил тяжести сохраняется проекция ее импульса на любое горизонтальное направление.

Теперь покажем, что если импульс системы сохраняется в одной инерциальной K - системе отсчета, то он сохраняется и в любой другой инерциальной K^/ - системе. Пусть в K – системе

.

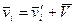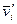Если K^/ -система движется относительно K - системы со скоростью , то скорость i -й частицы в K - системе можно представить как , где - скорость этой частицы в K^/ - системе. Тогда выражение для импульса системы можно преобразовать к следующему виду: 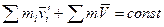. Вторая сумма в этом равенстве не зависит от времени. А это значит, что и первая сумма — импульс системы в K^/ - системе отсчета - тоже не зависит от времени, т. е.

.

Полученный результат полностью соответствует принципу относительности Галилея, согласно которому законы механики одинаковы во всех инерциальных системах отсчета.

Таким образом, закон сохранения импульса принадлежит к числу универсальных законов природы. Приращение импульса рассматриваемой системы может возникнуть только за счет убыли такой же величины импульса в окружающих телах (или поля излучения). Максимум, на что «способен» импульс в этом отношении — это перераспределяться между отдельными частями материи.

Дата добавления: 2014-11-29