Работа и мощность. Работа. Пусть частица под действием силы совершает перемещение по некоторой траектории 1 - 2 (рис

Работа. Пусть частица под действием силы совершает перемещение по некоторой траектории 1 - 2 (рис. 5.1). В общем случае сила в процессе движения частицы может меняться как по величине, так и по направлению. Рассмотрим элементарное перемещение 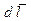, в пределах которого силу можно считать постоянной.

Действие силы на перемещении 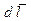характеризуют величиной, равной скалярному произведению 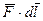, которую называют элементарной работой силы на перемещении .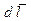

Ее можно представить и в другом виде:

,

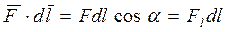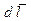где α — угол между векторами и , a 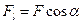- проекция вектора на перемещение .

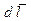Таким образом, элементарная работа 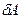силы на перемещении 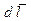определяется выражением

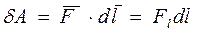. (5.1)

Величина 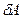- алгебраическая: в зависимости от угла между векторами и dl (или от знака проекции F_l вектора на вектор 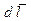) она может быть как положительной, так и отрицательной и, в частности, равной нулю (если ).

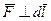Суммируя (интегрируя) выражение (5.1) по всем элементарным участкам пути от точки 1 до точки 2, можно найти работу силы на данном пути:

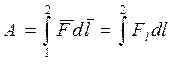. (5.2)

В частности, если на всем пути F_l = const, то А = F_l l, где l — путь.

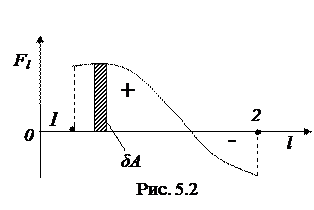Выражению (5.2) можно придать наглядный геометрический смысл. Изобразим график F_l как функцию положения частицы на траектории. Пусть, например, этот график имеет вид, показанный на рис. 5.2. Из этого рисунка видно, что элементарная работа 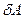численно равна площади заштрихованной полоски, а работа А на пути от точки 1 до точки 2 - площади фигуры, ограниченной кривой, вертикальными прямыми 1 и 2 и осью l. При этом площадь фигуры над осью l берется со знаком плюс (она соответствует положительной работе), а площадь фигуры под осью l - со знаком минус (она соответствует отрицательной работе).

Рассмотрим несколько примеров на вычисление работы.

1. Работа упругой силы 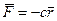, где - радиус-вектор частицы А относительно точки О (рис. 5.3). Переместим частицу А, на которую действует эта сила, по произвольному пути из точки 1 в точку 2. Вычислим сначала элементарную работу силы на элементарном перемещении :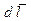

.

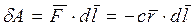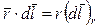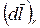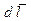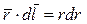Скалярное произведение , где - проекция вектора на вектор . Эта проекция равна, очевидно, dr – приращению модуля вектора . Поэтому и

.

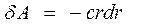Теперь вычислим работу этой силы на всем пути, т. е. проинтегрируем последнее выражение от точки 1 до точки 2:

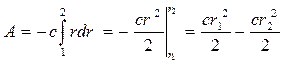. (5.3)

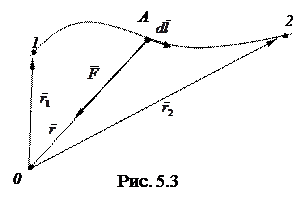2. Работа гравитационной (или кулоновской) силы. Пусть в точке О (см. рис. 5.3) находится неподвижная точечная масса (заряд). Найдем работу, совершаемую гравитационной (кулоновской) силой, при перемещении частицы А из точки 1 в точку 2 по произвольному пути. Сила, действующая на частицу А, может быть представлена так:

,

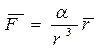где 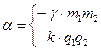- коэффициент, определяемый для гравитационного или кулоновского взаимодействия.

Вычислим сначала элементарную работу этой силы на перемещении :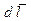

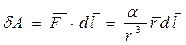
Как и в предыдущем случае, скалярное произведение 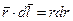, поэтому 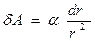. Работа этой силы на всем пути

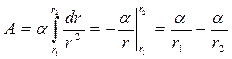. (5.4)

3. Работа однородной силы тяжести 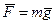. Запишем эту силу в ви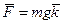де , где 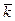орт вертикальной оси Z, положительное направление которой выбрано вверх. Элементарная работа этой силы на перемещении 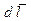равна

.

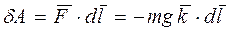Скалярное произведени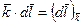е , где 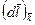- проекция вектора 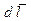на орт 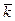. Эта проекция, очевидно, равна dz - приращению координаты Z. Поэтому 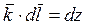и 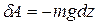. Работа же этой силы на всем пути от точки 1 до точки 2

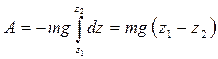. (5.5)

Рассмотренные силы интересны в том отношении, что их работа, как видно из формул (5.3) - (5.5), не зависит от формы пути между точками 1 и 2, а зависит только от положения этих точек. Эта весьма важная особенность данных сил присуща, однако, не всем силам. Например, сила трения этим свойством не обладает: работа этой силы зависит не только от положения начальной и конечной точек, но и от формы пути между ними.

До сих пор речь шла о работе одной силы. Если же на частицу в процессе движения действуют несколько сил, результирующая которых 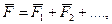то нетрудно показать, что работа результирующей силы на некотором перемещении равна алгебраической сумме работ, совершаемых каждой из сил в отдельности на том же перемещении. Действительно,

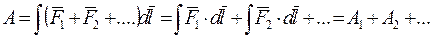. (5.6)

Мощность. Для характеристики интенсивности, с которой совершается работа, вводят величину, называемую мощностью. Мощность, - это работа, совершаемая силой за единицу времени. Если за промежуток времени dt сила совершает работу 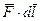, то мощность, развиваемая этой силой в данный момент времени, есть 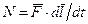. Учитывая, что 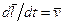, получим

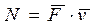. (5.7)

Таким образом, мощность, развиваемая силой , равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения данной силы. Как и работа, мощность - величина алгебраическая.

Зная мощность силы , можно найти и работу, которую совершает эта сила за промежуток времени t. В самом деле, представив подынтегральное выражение в (5.2) в виде 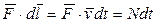, получим

.

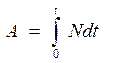В заключение обратим внимание на одно весьма существенное обстоятельство. Когда говорят о работе (или мощности), то необходимо в каждом конкретном случае четко указывать или представлять себе, работа какой именно силы (или сил) имеется в виду. В противном случае, как правило, неизбежны недоразумения.

Дата добавления: 2014-11-29