Столкновение двух частиц

В этом параграфе мы рассмотрим различные случаи столкновения двух частиц, используя в качестве инструмента исследования только законы сохранения импульса и энергии. При этом мы увидим, что законы сохранения позволяют сделать ряд общих и существенных заключений о свойствах данного процесса вне какой-либо зависимости от конкретного характера взаимодействия частиц.

Попутно мы покажем, какие преимущества дает Ц - система, использование которой, как будет видно, значительно упрощает анализ процесса и многие расчеты.

Хотя в этом параграфе будет идти речь о столкновении частиц, необходимо сразу же оговорить, что все последующие рассуждения и выводы в равной степени относятся и к столкновению любых тел.

Надо только иметь в виду, что вместо скорости частицы следует брать скорость центра инерции каждого тела, а вместо кинетической энергии частицы - ту часть кинетической энергии каждого тела, которая характеризует его движение как целого.

В дальнейшем будем считать:

1) исходная K - система отсчета инерциальная,

2) система из двух частиц замкнутая,

3) импульсы (и скорости) частиц до и после столкновения соответствуют достаточно большим расстояниям между ними, при этом потенциальной энергией взаимодействия можно просто пренебречь.

Кроме того, величины, относящиеся к системе после столкновения, будем отмечать штрихом, а величины в Ц – системе значком тильда (~) сверху.

Теперь перейдем к существу вопроса. Различают три типа столкновения частиц: абсолютно неупругое, абсолютно упругое и промежуточный случай — неупругое. Рассмотрим их последовательно.

Абсолютно неупругое столкновение, в результате которого обе частицы «слипаются» и далее движутся как единое целое. Пусть две частицы, массы которых т ₁ и т ₂, имеют до столкновения скорост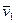и и 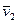(в K - системе). После столкновения образуется частица с массой т ₁ + т ₂, что прямо следует из аддитивности массы в ньютоновской механике. Скорость 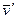образовавшейся частицы можно найти сразу из закона сохранения импульса:

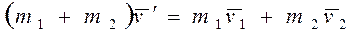
Ясно, что скорость 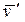равна скорости центра инерции системы.

В Ц - системе этот процесс выглядит наиболее просто: до столкновения обе частицы движутся навстречу друг другу с одинаковыми импульсами 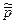, а после столкновения образовавшаяся частица оказывается неподвижной. При этом суммарная кинетическая энергия частиц 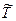целиком переходит во внутреннюю энергию 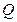образовавшейся частицы, т. е. 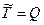. Отсюда с учетом формулы (6.21) найдем

.

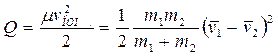Таким образом, величина Q для данной пары частиц зависит только от их относительной скорости.

Абсолютно упругое столкновение, в результате которого внутренняя энергия частиц не меняется, а поэтому не меняется и кинетическая энергия системы. Рассмотрим два частных случая: лобовое и нелобовое упругие столкновения.

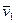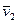1. Лобовое столкновение, при котором обе частицы до и после столкновения движутся по одной и той же прямой. Пусть до столкновения скорости частиц в K - системе отсчета равны и (частицы движутся или навстречу друг другу, или одна частица догоняет другую). Каковы скорости этих частиц после столкновения?

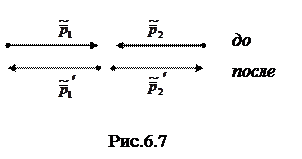Рассмотрим этот процесс сначала в Ц - системе, где до и после столкновения обе частицы имеют одинаковые по модулю и противоположные по направлению импульсы (рис. 6.7). Более того, так как суммарная кинетическая энергия частиц до и после столкновения одна и та же, равно как и их приведенная масса, то согласно (6.21) импульс каждой частицы в результате столкновения изменит только направление на противоположное, не меняясь при этом по модулю, т. е. 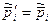, где i = 1,2. Последнее относится и к скорости каждой частицы в Ц - системе:

.

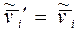Теперь найдем скорость каждой частицы после столкновения в K - системе отсчета. Для этого используем формулы преобразования скоростей при переходе от Ц - к K - системе, а также предыдущее равенство. Тогда

,

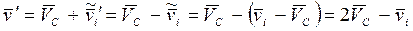где 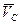- скорость центра инерции (Ц - системы) в К - системе отсчета; эта скорость определяется формулой (6.12).

Итак, скорость i -й частицы в K - системе после столкновения есть

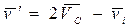(6.23)

где i = 1, 2.

В проекциях на произвольную ось X это равенство имеет вид

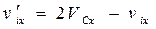. (6.24)

В частности, если массы частиц одинаковы, то легко убедиться, что частицы в результате столкновения просто обмениваются скоростями, т. е.

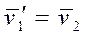и .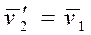

2. Нелобовое столкновение. Ограничимся случаем, когда одна из частиц покоится до столкновения. Пусть в K - системе отсчета частица массы т ₁ с импульсом 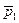испытала упругое нелобовое столкновение с покоившейся частицей массы т ₂. Каковы возможные импульсы этих частиц после столкновения?

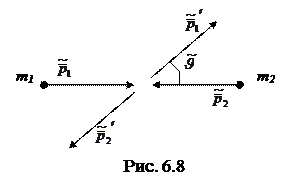Рассмотрим этот процесс также сначала в Ц - системе. Здесь, как и в предыдущем случае, обе частицы в любой момент времени до и после столкновения имеют одинаковые по модулю и противоположные по направлению импульсы. Кроме того, импульс каждой частицы не изменится по модулю в результате столкновения, т. е. .

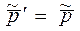Однако направление разлета частиц теперь будет иным. Оно повернется на некоторый угол 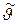(рис. 6.8), зависящий от характера взаимодействия частиц и их взаимного расположения в процессе столкновения.

Теперь найдем импульс каждой частицы в К - системе отсчета после столкновения. С помощью формул преобразования скоростей при переходе от Ц - к K - системе получим:

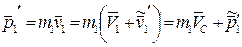
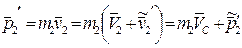(6.25)

где 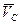- скорость Ц - системы относительно K - системы отсчета.

Сложив отдельно, левые и правые части этих равенств с учетом того, что 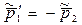, получим

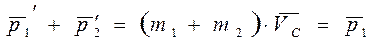
как и должно быть в соответствии с законом сохранения импульса.

Неупругое столкновение. Это такое столкновение, в результате которого внутренняя энергия разлетающихся частиц (или одной из них) изменяется, а следовательно, изменяется и суммарная кинетическая энергия системы. Соответствующее приращение кинетической энергии системы принято обозначать через Q. В зависимости от знака Q неупругое столкновение называют экзоэнергетическим (Q > 0) или эндоэнергетическим (Q < 0). В первом случае кинетическая энергия системы увеличивается, во втором - уменьшается. При упругом столкновении, разумеется, Q = 0.

Наша задача - найти возможные импульсы частиц после неупругого столкновения.

Этот вопрос наиболее просто решается в Ц - системе. Согласно условию, приращение суммарной кинетической энергии системы в данном процессе

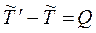. (6.26)

Так как в нашем случае 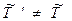, то это означает согласно (6.21), что импульсы частиц после столкновения изменятся по модулю. Импульс каждой частицы после столкновения 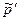легко найти, заменив 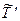в (6.26) его выражением 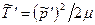. В результате получим

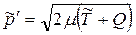. (6.27)

Порог. Существует много неупругих столкновений, в которых внутренняя энергия частиц способна изменяться только на совершенно определенную величину, зависящую от свойств самих частиц (таковы, например, неупругие столкновения атомов и молекул). Несмотря на это, экзоэнергетические столкновения (Q > 0) могут происходить при сколь угодно малой кинетической энергии налетающей частицы. Эндоэнергетические же процессы (Q < 0) в таких случаях обладают порогом. Порогом называют минимальную кинетическую энергию налетающей частицы, начиная с которой данный процесс становится энергетически возможным.

Итак, пусть нам необходимо осуществить такое эндоэнергетическое столкновение, в котором внутренняя энергия частиц способна получить приращение не меньше некоторого значения | Q|. При каком условии такой процесс окажется возможным?

Этот вопрос наиболее просто решается также в Ц - системе, где ясно, что суммарная кинетическая энергия частиц до столкновения 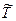во всяком случае должна быть не меньше | Q |, т. е. 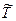>- Q|. Отсюда следует, что существует минимальное значение 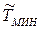= |Q|, при котором кинетическая энергия системы целиком пойдет на увеличение внутренней энергии частиц и частицы после столкновения остановятся в Ц -системе.

Рассмотрим этот же вопрос в К -системе отсчета, где частица массы т₁ налетает на покоящуюся частицу массы т₂. Так как в Ц - системе при 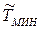частицы после столкновения останавливаются, то это значит, что в К -системе при соответствующей пороговой кинетической энергии налетающей частицы 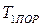обе частицы после столкновения будут двигаться как единое целое. Причем с суммарным импульсом, равным импульсу налетающей частицы, и кинетической энергией 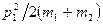. Поэтому

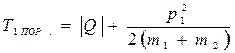
А так как 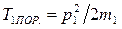, то, исключив 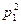из этих двух уравнений, получим

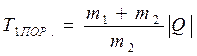(6.30)

Это и есть та пороговая кинетическая энергия налетающей частицы, начиная с которой данный эндоэнергетический процесс становится энергетически возможным. Заметим, что формула (6.30) играет большую роль особенно в атомной и ядерной физике. С помощью нее определяют как порог различных эндоэнергетических процессов, так и соответствующее им значение энергии

В заключение рассмотрим пример, который по существу является моделью эндоэнергетического столкновения.

Задача 6.10

На гладкой горизонтальной плоскости находятся небольшая шайба массы т и гладкая горка массы М и высоты h (рис. 6.9). Какую минимальную скорость необходимо сообщить шайбе, чтобы она смогла преодолеть эту горку?

Ясно, что скорость шайбы должна быть по крайней мере такой, чтобы она смогла подняться на вершину горки и далее двигаться вместе с горкой как единое целое.

При этом часть кинетической энергии системы пойдет на приращение потенциальной энергии

Δ U = mgh.

Будем рассматривать этот процесс как зндоэнергетический, где |Q | - Δ U. Тогда согласно последней формуле

,

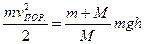откуда

.

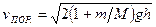Вывод

Сформулировано понятие импульса частицы и системы частиц. Одна из основных теорем динамики раскрыта с позиции закона сохранения импульса системы и записана в дифференциальной форме. Предложен пример движения тела с переменной массой и введением понятия реактивной силы. Теория импульса изложена для замкнутой и незамкнутой систем. В этой же постановке рассмотрено изменение импульса при столкновении частиц.

Контрольные вопросы

1. Сформулируйте понятия импульса частицы и системы.

2. Запишите закон сохранений импульса тела с использованием понятия количества движения.

3. Сформулируйте уравнение И.В.Мещерского.

4. Что такое центр инерции?

5. Дайте определение Ц-системе.

6. Укажите различия абсолютно упругого и абсолютно неупругого столкновения частиц.

7. Дайте определение порогового столкновения частиц.

Глава 7 ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Дата добавления: 2014-11-29