Собственный момент импульса системы

В предыдущем параграфе было установлено, что момент импульса системы изменяется только под действием суммарного момента всех внешних сил; именно этот вектор определяет поведение вектора . Теперь рассмотрим некоторые наиболее существенные свойства этих величин и те важные выводы, которые из них вытекают.

Суммарный момент внешних сил. Как и момент каждой силы, суммарный момент сил зависит, вообще говоря, от выбора точки, относительно которой его определяют. Пусть - суммарный момент сил относительно точки

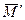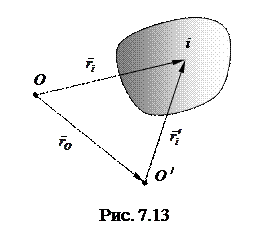
О, а - относительно точки О', радиус-вектор которой равен 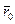(рис. 7.13). Найдем связь между и .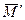

Радиусы - векторы 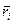и 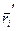точки приложения силы 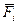связаны соотношением 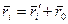(см. рис. 7.13). Поэтому выражение для можно записать в таком виде:

,

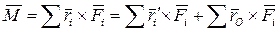или

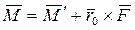, (7.18)

где 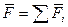- результирующая всех внешних сил.

Из формулы (7.18) видно, что если 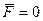, то суммарный момент внешних сил не зависит от выбора точки, относительно которой его определяют. В этом случае говорят, что к системе приложена пара сил с моментом .

Интересной и важной особенностью в этом отношении обладает Ц - система (напомним, что эта система отсчета жестко связана с центром инерции системы частиц и перемещается поступательно по отношению к инерциальным системам). Так как в общем случае Ц - система является неинерциальной, то результирующая всех внешних сил должна включать в себя кроме внешних сил взаимодействия 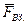, и силы инерции 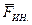. С другой стороны, в Ц - системе система частиц как целое покоится, а это значит согласно (6.14), что 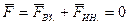. Имея в виду (7.18), мы приходим к следующему важному выводу: в Ц - системе суммарный момент всех внешних сил, включая силы инерции, не зависит от выбора точки О.

И другой важный вывод: в Ц - системе суммарный момент сил инерции относительно центра инерции всегда равен нулю:

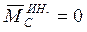. (7.19)

В самом деле, сила инерции, действующая на каждую частицу системы, имеет вид 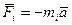, где 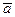- ускорение Ц - системы. Поэтому суммарный момент всех этих сил относительно центра инерции С можно записать таким образом:

.

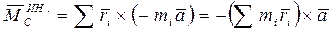Согласно (6.11), сумма, стоящая в круглых скобках, равна 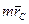, а так как в нашем случае 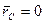, то и .

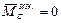Собственный момент импульса. Как и момент сил, момент импульса системы зависит, вообще говоря, от выбора точки О, относительно которой его определяют. При переносе этой точки на расстояние 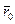(см. рис. 7.13) новые радиусы-векторы частиц 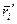связаны со старыми 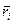; формулой 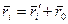. Поэтому момент импульса системы относительно точки О можно представить так:

,

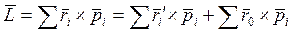или

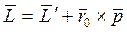(7.20)

где 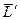- момент импульса системы относительно точки О', а 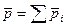- полный импульс системы.

Из формулы (7.20) следует, что если полный импульс системы 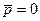, то ее момент импульса не зависит от выбора точки О. А этим как раз и отличается Ц - система, в которой система частиц как целое покоится. Отсюда мы приходим к третьему важному выводу: в Ц - системе момент импульса системы частиц не зависит от выбора точки, относительно которой его определяют. Этот момент будем называть собственным моментом импульса системы и обозначать .

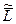Задача 7.9

Найдем выражение для собственного момента импульса системы из двух частиц.

Воспользовавшись тем обстоятельством, что в Ц - системе собственный момент импульса 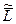не зависит от выбора точки О, возьмем эту точку совпадающей в данный момент времени с одной из частиц, например с частицей 2 (рис. 7.14). Тогда

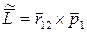. (7.21)

где 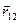- радиус-вектор, характеризующий положение частицы 1 относительно частицы 2, 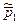- импульс частицы 1 в Ц -системе.

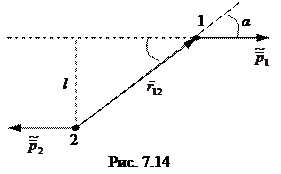Поскольку в Ц -системе 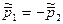предыдущее выражение можно записать и так:

,

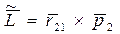где 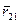- радиус-вектор частицы 2 относительно частицы 1, причем .

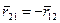Модуль вектора 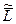равен 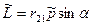, α - угол между векторам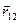и и 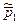(см. рис. 85). Учитывая, что 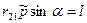, где l - плечо вектора 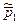относительно точки, в которой находится частица 2, перепишем выражение для 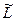в таком виде:

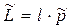. (7.22)

Таким образом, модуль собственного момента импульса системы из двух частиц равен произведению плеча l вектора 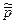одной из частиц относительно точки, в которой находится другая частица, на модуль импульса частицы 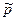в Ц -системе.

Связь между и 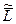. Пусть - момент импульса системы частиц относительно точки О K - системы отсчета. Так как собственный момент импульса в Ц - системе не зависит от выбора точки О', возьмем точку О' совпадающей в данный момент с точкой О K -системы. Тогда радиус-векторы каждой частицы в обеих системах отсчета будут одинаковы в этот момент (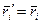), скорости же частиц связаны формулой 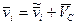, где 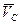- скорость Ц - системы относительно K -системы. Поэтому можно записать:

.

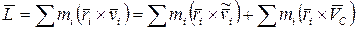Первая сумма в правой части этого равенства есть собственный момент импульса 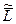. Вторую сумму в соответствии с формулой (6.11) представим как

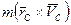, или 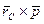, где m - масса всей системы, 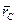- радиус-вектор ее центра инерции в K -системе, 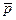- суммарный импульс системы. В результате

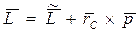. (7.23)

Таким образом, момент импульса системы частиц в K - системе отсчета складывается из ее собственного момента импульса 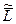и момента 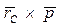, связанного с движением системы частиц как целого.

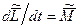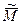Уравнение моментов в Ц -системе. В предыдущем параграфе было отмечено, что уравнение (7.14) справедливо в любой системе отсчета. Значит, оно справедливо и в Ц - системе. Поэтому сразу можно записать: , где - суммарный момент внешних сил в Ц -системе.

Так как Ц - система в общем случае неинерциальная, то в 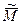входит помимо моментов внешних сил взаимодействия и момент сил инерции. С другой стороны, в начале этого параграфа было показано, что момент сил 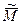в Ц - системе не зависит от выбора точки, относительно которой его определяют. Обычно в качестве такой точки берут точку С - центр инерции системы. Целесообразность выбора именно этой точки в том, что относительно нее суммарный момент сил инерции равен нулю, и поэтому следует учитывать только суммарный момент внешних сил взаимодействия 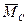. Итак,

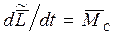, (7.24)

т. е. производная по времени от собственного момента импульса системы равна суммарному моменту всех внешних сил взаимодействия относительно центра инерции данной системы.

В частности, если 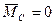, то 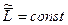, что выражает закон сохранения собственного момента импульса системы.

В проекциях на ось Z, проходящую через центр инерции системы, уравнение (7.24) имеет вид

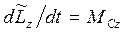(7.25),

где 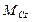- суммарный момент внешних сил взаимодействия относительно неподвижной в Ц - системе оси z, проходящей через центр инерции. И здесь если 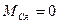, то .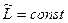

Дата добавления: 2014-11-29