П.1.6 Бином Ньютона

При п натуральном имеет место формула

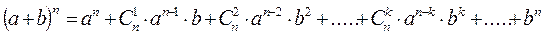
Свойства биномиальных коэффициентов:

- коэффициенты членов, равноотстоящих от концов, равны между собой;

- сумма всех коэффициентов равна 2 ⁿ;

- сумма коэффициентов членов, стоящих на нечетных местах, равна сумме коэффициентов членов, стоящих на четных местах.

Формула бинома может быть распространена на отрицательные и дробные показатели; при этом получается в правой части равенства бесконечный ряд.

П.1.7 Определители (детерминанты)

Определителем второго порядка называется число D_, образованное из четырех чисел, расположенных в квадратную таблицу, и вычисляемое по формуле

.

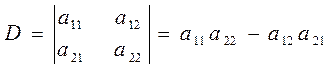Вообще определителем n – го порядка называется число, образованное из n² чисел, расположенных в квадратную матрицу

,

и равное сумме n! членов, каждый из которых является произведением п элементов, взятых по одному (итолько одному) из каждой строки и каждого столбца; знак каждого произведения равен (—1) ^t, где t — число инверсий в перестановке, составленной из вторых индексов, если первые индексы расположены в возрастающем порядке. (В данной перестановке числа i и j составляют инверсию, если i > j, но j стоит в этой перестановке после i).

Например, для определителя третьего порядка имеем

;

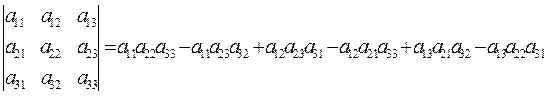число слагаемых равно 3!, т. е. 6; первые индексы следуют в порядке 1, 2, 3; во вторых индексах имеется шесть перестановок; в первом слагаемом нет инверсий, во втором — одна инверсия (32), в третьем — две инверсии (21 и 31) и т. д.

Свойства определителей:

1) при замене строк столбцами величина определителя не меняется;

2) при перестановке двух столбцов или строк определитель меняет знак;

3) определитель с двумя одинаковыми столбцами (или строками) равен нулю;

4) множитель, общий для элементов некоторого столбца или строки, можно вынести за знак определителя;

5) величина определителя не изменится, если к элементам некоторого столбца или строки прибавить элементы параллельного столбца или строки, предварительно умножив эти последние на один и тот же произвольный множитель l.

Вычисление определителя можно свести к вычислению определителей порядка на единицу ниже. Назовем минором элемента 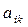определитель, получаемый вычеркиванием i – й строки и k - гoстолбца данного определителя. Назовем адъюнктой (или алгебраическим дополнением) элемента его минор, умноженный на (—1) ^i+k; обозначим адъюнкту элемента через .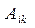

Разложив определитель по элементам i - й. строки, имеем

.

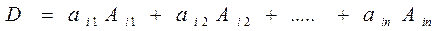Дата добавления: 2014-11-29