Основные законы ньютоновской динамики

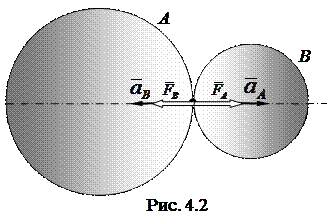Понятия о силе и массе. Изучая на опыте различные движения, мы обнаруживаем, что в инерциальных системах отсчета всякое ускорение тела вызывается действием на него каких-либо других тел. Кроме того, во всех случаях, когда в опыте участвуют только два тела А и В и тело А сообщает ускорение телу В, то и тело В также сообщает ускорение телу А (рис. 4.2). Отсюда мы заключаем, что действия тел друг на друга имеют характер взаимодействия.

Для характеристики этого взаимодействия вводят новую фундаментальную величину – силу , которая служит мерой механического взаимодействия тел. Поскольку сила является причиной ускорения, а ускорение обладает свойствами вектора, то постулируется, что и сила есть вектор, причем направленный так же, как и ускорение 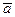, вызываемое этой силой , т. е. .

Одной из важнейших характеристик силы является ее материальное происхождение. Говоря о силе, мы всегда неявно предполагаем, что в отсутствие посторонних тел сила, действующая на интересующее нас тело, равна нулю. Если же обнаруживается, что сила действует, мы ищем ее источник в виде того или иного конкретного тела или других тел.

Все силы, с которыми имеет дело механика, обычно подразделяют на силы, возникающие при непосредственном контакте тел (силы давления, трения), и силы, возникающие через посредство создаваемых взаимодействующими телами полей (силы гравитационные, электромагнитные). Заметим, однако, что такое подразделение сил имеет условный характер: в сущности, и при непосредственном контакте силы взаимодействия обусловлены также наличием тех или иных полей, создаваемых молекулами или атомами тел. Таким образом, все силы взаимодействия между телами обусловлены, в конечном счете, полями. Вопрос о природе сил взаимодействия выходит за рамки механики и рассматривается в разделах физики. В механике же ограничиваются лишь рассмотрением того, какие силы возникают в том или ином конкретном случае.

Вводя новую физическую величину, мы должны, прежде всего, установить способ ее измерения, т. е. способ сравнения этой величины с эталоном. Выясним, как это можно сделать по отношению к силе.

Основной статическийспособ измерения силы, действующей на некоторую материальную точку, заключается в уравновешивании ее действием на ту же точку определенным образом деформированной пружины-эталона, служащей эталоном силы. Если в результате совместного действия этих двух сил материальная точка будет покоиться или двигаться без ускорения (в инерциальной системе отсчета), мы утверждаем, что измеряемая сила равна по модулю эталону силы и направлена противоположно последней. Имея в своем распоряжении несколько одинаковых эталонных пружин и располагая их параллельно или под разными углами, в принципе можно уравновесить, а, следовательно, и измерить любую силу. Этим способом можно установить, что сила как вектор действительно подчиняется обычному правилу сложения векторов, а также найти зависимости ряда сил от различных величин.

Статический способ измерения сил имеет, однако, ограниченную применимость: он не дает возможности определить силы, действующие на тело в процессе его движения. Выход из этого затруднения дает опыт, который показывает, что ускорения, приобретаемые одним и тем же телом под действием разных сил, пропорциональны этим силам, будучи измеренным статическим способом. Отсюда вытекает динамический способ сравнения сил по вызываемым ими ускорениям:

.

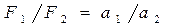Этот способ позволяет установить законы сил, которые невозможно или трудно измерить статически.

Далее, опыт показывает, что при любой по величине и направлению силе отношение F/а для данного тела остается постоянным. Для разных же тел это отношение оказывается различным. Отсюда вывод: величина отношения F/а характеризует некоторое свойство тел, а именно инертность, которая выражает степень неподатливости тела к изменению его скорости.

Для количественной характеристики инертности тела вводят новую физическую величину т, пропорциональную отношению F/а. Эту величину т называют массой. Из определения т ~ F/а вытекает способ сравнения масс: при одинаковой силе отношение масс двух тел равно обратному отношению их ускорений:

т₁ / т₂= а₂ / а₁.

Взяв определенное тело за эталон массы, мы имеем возможность, таким образом, сравнить массу любого тела с этим эталоном.

Опыт показывает, что в рамках классической механики масса обладает следующими двумя важнейшими свойствами:

1) масса - величина аддитивная, т. е. масса составного тела равна сумме масс его частей;

2) масса тела как такового - величина постоянная, не изменяющаяся при его движении.

Основные законы динамики. Обобщение результатов опыта составляет содержание второго и третьего законов Ньютона.

Второй закон Ньютона. Ускорение материальной точки в инерциальной системе отсчета прямо пропорционально действующей на нее силе и обратно пропорционально ее массе. При надлежащем выборе единиц измерения величин это утверждение записывают математически так:

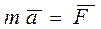, (4.5)

где в общем случае есть равнодействующая всех сил, приложенных к данной материальной точке, .

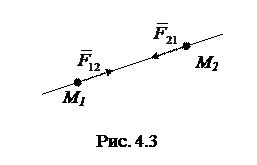Третий закон Ньютона. Всякое действие тел друг на друга носит характер взаимодействия. Две материальные точки действуют друг на друга с силами, равными по величине и направленными в противоположные стороны вдоль прямой, соединяющей эти точки (рис. 4.3), т. е.

. (4.6)

Здесь предполагается, что обе силы равны по величине в любой момент времени независимо от движения точек. Это утверждение соответствует ньютоновскому представлению о мгновенном распространении взаимодействий - предположению, которое носит название принципа дальнодействия классической механики. Согласно этому принципу взаимодействие между телами распространяется в пространстве с бесконечно большой скоростью. Иначе говоря, если изменить положение (состояние) одного тела, то сразу же можно обнаружить хотя бы очень слабое изменение во взаимодействующих с ним телах, как бы далеко они ни находились.

Сейчас мы знаем, что в действительности это не так - существует конечная максимальная скорость распространения взаимодействий, которая равна скорости света в пустоте. Поэтому третий закон Ньютона (а также и второй) имеет определенные пределы применимости. Однако при скоростях тел, значительно меньших скорости света, с которыми имеет дело классическая механика, оба закона выполняются с очень большой точностью. Свидетельством этому являются хотя бы расчеты траекторий планет и искусственных спутников, которые проводятся с «астрономической» точностью именно с помощью законов Ньютона.

Законы Ньютона являются основными законами классической механики. Они позволяют, по крайней мере, в принципе, решить любую механическую задачу; кроме того, из них могут быть выведены и все остальные законы классической механики.

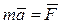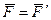В соответствии с принципом относительности Галилея законы механики одинаковы во всех инерциальных системах отсчета. Это значит, в частности, что уравнение (4.5) будет иметь один и тот же вид в любых двух инерциальных системах K и K': и . Из независимости массы данной материальной точки от скорости следует, что т = т¹. Кроме того, для инерциальных систем отсчета . Отсюда вытекает, что , т. е. при переходе от одной инерциальной системы отсчета к другой сила не меняется.

Итак, все величины, входящие в уравнение второго закона Ньютона, не меняются при переходе от одной инерциальной системы отсчета к другой. Другими словами, уравнения Ньютона инвариантны относительно преобразований Галилея.

Дата добавления: 2014-11-29