
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
К другой системе отсчета
|
|
|
|
Преобразования скорости и ускорения при переходе
Приступая к изучению этого вопроса, напомним, что в рамках классической механики длина масштабов и время считаются абсолютными. Любой масштаб одинаков в разных системах отсчета, т. е. не зависит от движения. Это же касается и течения времени, которое также одинаково во всех системах.
Постановка вопроса. Имеются две произвольные системы отсчета, K – неподвижна, и K', которая движется относительно К. Известны скорость 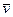 и ускорение
и ускорение 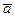 некоторой точки А в K – системе (рис. 3.19). Так как движение точки А является сложным, введем следующие определения. Движение точки относительно системы координат K назовем абсолютным – обозначим индексом - а. Движение точки А относительно системы координат K' назовем относительным обозначим индексом – r. Движение системы K' относительносистемы координат K назовем переносным, обозначим индексом – е. Соответственно скорости и ускорения обозначим:
некоторой точки А в K – системе (рис. 3.19). Так как движение точки А является сложным, введем следующие определения. Движение точки относительно системы координат K назовем абсолютным – обозначим индексом - а. Движение точки А относительно системы координат K' назовем относительным обозначим индексом – r. Движение системы K' относительносистемы координат K назовем переносным, обозначим индексом – е. Соответственно скорости и ускорения обозначим:
 .
.
При абсолютном значении скорости и ускорения индекс a обычно опускают.
Каковы соответствующие значения 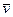 и
и 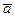 точки А в K - системе?
точки А в K - системе?
Рассмотрим последовательно три наиболее важных случая движения одной системы отсчета относительно другой.
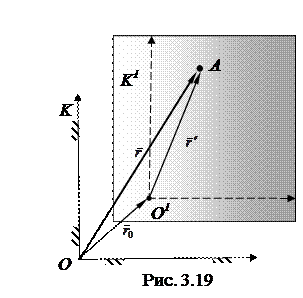 Случай I. K' - система движется поступательно по отношению к K -системе. Пусть в K - системе начало отсчета K / - системы характеризуется радиус-вектором
Случай I. K' - система движется поступательно по отношению к K -системе. Пусть в K - системе начало отсчета K / - системы характеризуется радиус-вектором  . Положение точки А в K - системе определяется радиусом-вектором
. Положение точки А в K - системе определяется радиусом-вектором  , а в K' – системе - радиусом-вектором
, а в K' – системе - радиусом-вектором 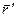 , тогда
, тогда 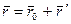 (рис. 3.19). За промежуток времени dt точка А совершит в K - системе элементарное перемещение
(рис. 3.19). За промежуток времени dt точка А совершит в K - системе элементарное перемещение 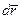 . Это перемещение складывается из перемещения
. Это перемещение складывается из перемещения 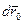 вместе с K' - системой и перемещения
вместе с K' - системой и перемещения 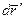 относительно K' - системы, т. е.
относительно K' - системы, т. е.
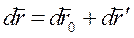 .
.
Поделив данное выражение на dt, получим следующую формулу преобразования скорости 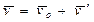 или с учетом введенных обозначений:
или с учетом введенных обозначений:
 . (3.21)
. (3.21)
Продифференцировав (3.21) по времени, сразу же найдем и формулу преобразования ускорения:
 . (3.22)
. (3.22)
Отсюда видно в частности, что при 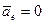
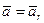 , т. е. при движении K' - системы без ускорения, относительно K - системы ускорение точки А в обеих системах отсчета будет, одно и то же.
, т. е. при движении K' - системы без ускорения, относительно K - системы ускорение точки А в обеих системах отсчета будет, одно и то же.
Задача 3.8
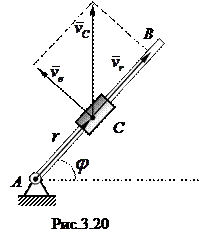
Кулиса АВ вращается в плоскости вокруг неподвижной точки А с угловой скоростью ω. Кулисный камень С скользит вдоль кулисы со скоростью v. Найти его абсолютную скорость (рис. 3.20).
Решение. Точка С совершает сложное движение. Она перемещается вместе с кулисой и, кроме того, движется вдоль кулисы. Относительно кулисы точка С совершает прямолинейное движение со скоростью v. Приняв за подвижную систему отсчета кулису АВ, получим следующее значение относительной скорости точки С:
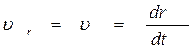 .
.
Вращение кулисы АВ является для точки С переносным движением, а потому переносная скорость этой точки будет:
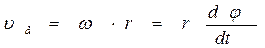 .
.
Поскольку в рассматриваемой задаче векторы переносной и относительной скоростей ортогональны друг другу, будем иметь:
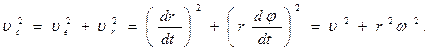
Случай II. K' - система вращается с постоянной угловой скоростью 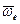 вокруг оси, неподвижной в K - системе.
вокруг оси, неподвижной в K - системе.
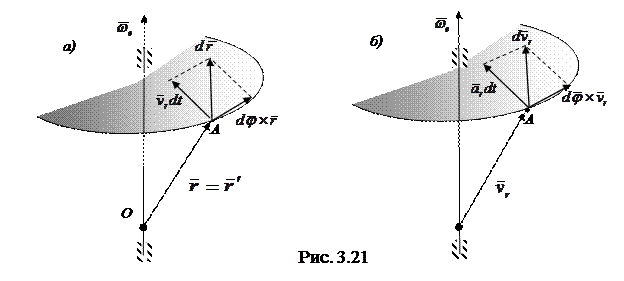 Возьмем начала отсчета K и K' - систем в произвольной точке О на оси вращения (рис. 3.21,а). Тогда радиус-вектор точки А в обеих системах отсчета будет один и тот же:
Возьмем начала отсчета K и K' - систем в произвольной точке О на оси вращения (рис. 3.21,а). Тогда радиус-вектор точки А в обеих системах отсчета будет один и тот же:  .
.
Если точка А неподвижна в K' - системе, то это значит, что приращение радиуса-вектора 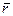 в K - системе за время dt обусловлено только его поворотом на угол
в K - системе за время dt обусловлено только его поворотом на угол 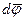 (вместе с K' - системой) и равно согласно (3.11) векторному произведению
(вместе с K' - системой) и равно согласно (3.11) векторному произведению 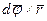 . Если же точка А движется относительно K' - системы со скоростью
. Если же точка А движется относительно K' - системы со скоростью 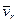 , то приращение
, то приращение 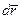 вектора
вектора  в K - системе будет складываться из его приращения
в K - системе будет складываться из его приращения 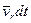 в K' - системе и приращения
в K' - системе и приращения 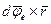 , связанного с поворотом K' - системы на угол dφ
, связанного с поворотом K' - системы на угол dφ
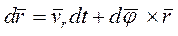 . (3.23)
. (3.23)
Поделив это выражение на dt, получим следующую формулу преобразования скорости:
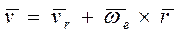 , (3.24)
, (3.24)
где  и
и 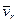 - скорость точки А в K - и K '-системах отсчета.
- скорость точки А в K - и K '-системах отсчета.
Теперь перейдем к ускорениям. В соответствии с (3.24) приращение 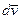 вектора
вектора  за время dt в K -системе должно складываться из суммы приращений векторов
за время dt в K -системе должно складываться из суммы приращений векторов 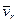 и
и 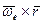 - при
- при 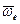 = const, т. е.
= const, т. е.
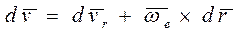 .(3.25)
.(3.25)
Если точка А движется в K' - системе c 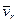 = const, то приращение этого вектора в K - системе обусловлено только его поворотом на угол
= const, то приращение этого вектора в K - системе обусловлено только его поворотом на угол 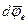 (вместе с K ' - системой) и равно, как и в случае с
(вместе с K ' - системой) и равно, как и в случае с  , векторному произведению
, векторному произведению 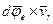 . В этом нетрудно убедиться, совместив начало вектора
. В этом нетрудно убедиться, совместив начало вектора 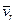 с осью вращения (см. рис. 3.21,б). Если же точка А имеет ускорение
с осью вращения (см. рис. 3.21,б). Если же точка А имеет ускорение 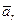 в K' -системе, то за время dt вектор
в K' -системе, то за время dt вектор 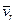 получит еще дополнительное приращение
получит еще дополнительное приращение 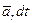 и тогда
и тогда
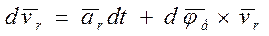 . (3.26)
. (3.26)
Теперь остается подставить (3.26) и (3.23) в равенство (3.25) и полученное выражение разделить на dt. В результате найдем следующую формулу преобразования ускорения:
 , (3.27)
, (3.27)
где 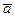 и
и 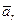 - ускорения точки А в K - и K ' - системах отсчета.
- ускорения точки А в K - и K ' - системах отсчета.
Второе слагаемое в правой части этой формулы носит название кориолисова (или поворотного) ускорения, а третье слагаемое - осестремительного ускорения:
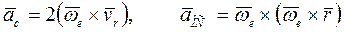 . (3.28)
. (3.28)
Осестремительное ускорение не следует путать с нормальным или центростремительным ускорением.
Таким образом, ускорение 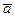 точки относительно K -системы равно сумме трех ускорений: ускорения
точки относительно K -системы равно сумме трех ускорений: ускорения 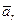 относительно K1 -системы, кориолисова ускорения
относительно K1 -системы, кориолисова ускорения  и осестремительного ускорения
и осестремительного ускорения 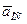 .
.
Осестремительное ускорение можно представить в виде
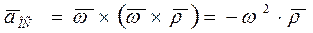 ,
,
где 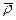 - радиус-вектор, перпендикулярный к оси вращения и характеризующий положение точки А относительно этой оси.
- радиус-вектор, перпендикулярный к оси вращения и характеризующий положение точки А относительно этой оси.
Тогда формулу (3.27) можно записать так:
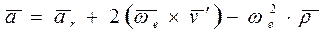 . (3.29)
. (3.29)
Случай III. K' - система вращается с постоянной угловой скоростью 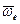 вокруг оси, перемещающейся поступательно со скоростью
вокруг оси, перемещающейся поступательно со скоростью 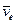 и ускорением
и ускорением 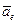 no отношению к K - системе.
no отношению к K - системе.
Этот случай объединяет два предыдущих. Введем вспомогательную S - систему отсчета, которая жестко связана с осью вращения K' - системы и перемещается поступательно в K - системе. Пусть 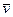 и
и  - скорости точки А в К и S - системах отсчета, тогда в соответствии с (3.21)
- скорости точки А в К и S - системах отсчета, тогда в соответствии с (3.21)  . Заменив
. Заменив  согласно (3.24) выражением
согласно (3.24) выражением 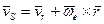 , где
, где  - радиус-вектор точки А относительно произвольной точки на оси вращения K' - системы, получим следующую формулу преобразования скорости:
- радиус-вектор точки А относительно произвольной точки на оси вращения K' - системы, получим следующую формулу преобразования скорости:
 . (3.30)
. (3.30)
Аналогичным образом, используя (3.22) и (3.29), найдем формулу преобразования ускорения:
 , (3.31)
, (3.31)
Обозначим 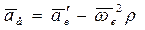 , тогда полученную формулу (3.31) можно записать как
, тогда полученную формулу (3.31) можно записать как
 . (3.32)
. (3.32)
Напомним, что в последних двух формулах 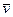 ,
, 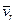 и
и 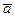 ,
, 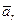 - скорость и ускорение точки A соответственно в K - и K' - системах отсчета,
- скорость и ускорение точки A соответственно в K - и K' - системах отсчета, 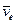 и
и 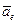 - скорость и ускорение оси вращения K' - системы в K - системе,
- скорость и ускорение оси вращения K' - системы в K - системе,  - радиус-вектор точки A относительно произвольной точки на оси вращения K' - системы,
- радиус-вектор точки A относительно произвольной точки на оси вращения K' - системы, 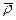 - радиус-вектор, перпендикулярный к оси вращения и характеризующий положение точки A относительно этой оси.
- радиус-вектор, перпендикулярный к оси вращения и характеризующий положение точки A относительно этой оси.
Модуль и направление ускорения Кориолиса. Правило Жуковского. Итак, ускорение Кориолиса равно удвоенному векторному произведению угловой (переносной) скорости подвижной системы отсчета - 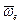 на относительную скорость точки -
на относительную скорость точки - 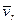 :
:
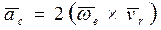
Модуль ускорения Кориолиса подсчитывают по формуле
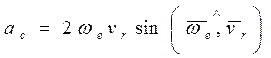 . (3.33)
. (3.33)
Направление ускорения 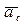 перпендикулярно к плоскости, проходящей через векторы
перпендикулярно к плоскости, проходящей через векторы 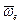 и
и  , в ту сторону, чтобы, глядя навстречу ему, мы видели бы поворот вектора
, в ту сторону, чтобы, глядя навстречу ему, мы видели бы поворот вектора 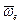 к вектору
к вектору  на наименьший угол происходящим против часовой стрелки (рис. 3.22а)).
на наименьший угол происходящим против часовой стрелки (рис. 3.22а)).
Направление ускорения Кориолиса можно также определить по правилу, предложенному Н. Е. Жуковским, проведя плоскость П, перпендикулярную к угловой скорости переносного вращательного движения (рис. 3.22б)).
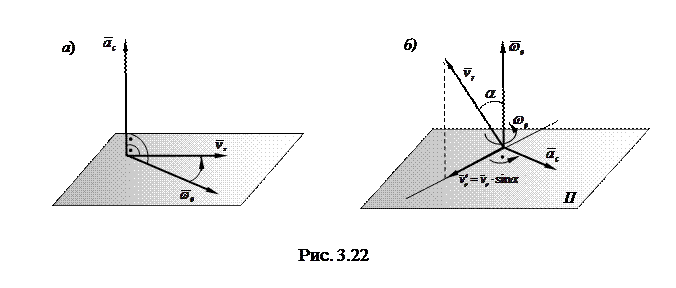
Правило Жуковского. Для определения направления ускорения Кориолиса необходимо вектор относительной скорости точки  спроецировать на плоскость П, перпендикулярную вектору
спроецировать на плоскость П, перпендикулярную вектору 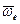 , затем проекцию-
, затем проекцию-  повернуть в направлении переносного вращения на 90°. Равенство
повернуть в направлении переносного вращения на 90°. Равенство  = 0, может быть в следующих случаях:
= 0, может быть в следующих случаях:
1) 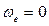 , т. е. подвижная система отсчета движется поступательно;
, т. е. подвижная система отсчета движется поступательно;
2)  , т. е. относительная скорость точки равна нулю (точка находится в относительном покое);
, т. е. относительная скорость точки равна нулю (точка находится в относительном покое);
3)  , т.е. угол между векторами
, т.е. угол между векторами 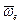 и
и 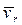 равен 0 и 1800.
равен 0 и 1800.
Задача 3.9
Диск радиусом СМ = R = 50 см вращается из состояния покоя с постоянным угловым ускорением ε = 0,2 с-2 в направлении, обратном направлению вращения часовой стрелки. По ободу диска в направлении, обратном его вращению, движется точка М с постоянной относительной скоростью vr - 50 см/с (рис. 3.33). Определить абсолютную скорость и абсолютное ускорение точки М в конце 5-й секунды.
Решение. Свяжем подвижную систему отсчета с вращающимся диском, а неподвижную - с Землей; движение точки М вместе с диском будет переносным движением, а ее движение по отношению к диску – относительным.
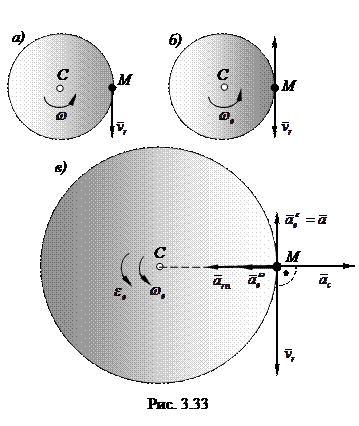 Абсолютное движение точки М состоит из этих двух движений. Так
Абсолютное движение точки М состоит из этих двух движений. Так
как диск вращается равноускоренно, его угловая скорость определяется выражением:
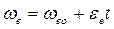 ,
,
где 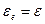 .
.
Учитывая, что диск вращается из состояния покоя, т.е. 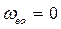 , находим модуль его угловой скорости в конце 5-й с:
, находим модуль его угловой скорости в конце 5-й с:
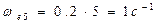 .
.
1. Определяем, абсолютную скорость точки М. Абсолютная скорость точки М определяется как геометрическая сумма двух скоростей: переносной скорости точки, равной скорости точки обода диска, и относительной скорости точки
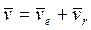 .
.
Вычислим модуль переносной скорости точки в конце 5-й с:
 .
.
Эта скорость направлена по касательной к окружности обода в сторону вращения диска, т. е. противоположно относительной скорости 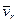 (рис. 3.33). В конце 5-й с:
(рис. 3.33). В конце 5-й с:
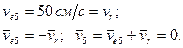
Модуль относительной скорости постоянен, а модуль переносной скорости возрастает равномерно от нуля. Следовательно, при t < 5 с ve < vr, направление  совпадает с направлением
совпадает с направлением 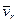 ; при t = 5 с ve = vr,
; при t = 5 с ve = vr,  = 0; при t > 5 с ve > vr, направление
= 0; при t > 5 с ve > vr, направление  совпадает с направлением
совпадает с направлением 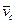 .
.
2. Определяем, абсолютное ускорение точки М. Абсолютное ускорение точки при вращательном переносном движении определяется по формуле:
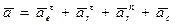 .
.
В рассматриваемой задаче переносное ускорение точки М равно ускорению той точки диска, которая в данный момент совпадает с точкой М. Траекторией этой точки диска, является окружность обода. Эта же окружность является и траекторией абсолютного движения точки М.
Переносное вращательное ускорение точки 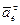 направлено по касательной к этой окружности соответственно
направлено по касательной к этой окружности соответственно 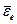 , а его модуль
, а его модуль
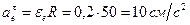 .
.
Переносное центростремительное ускорение точки 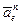 направлено по радиусу МС к центру окружности, а его модуль
направлено по радиусу МС к центру окружности, а его модуль
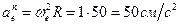 .
.
Так как относительное движение точки - движение равномерное, то относительное касательное ускорение равно нулю:
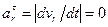 .
.
Относительное нормальное ускорение точки 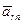 направлено по радиусу МС к центру кривизны траектории относительного движения, а его модуль
направлено по радиусу МС к центру кривизны траектории относительного движения, а его модуль
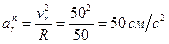 .
.
Модуль поворотного ускорения точки М вычисляем по формуле:
 .
.
Так как относительное движение происходит в плоскости, перпендикулярной оси переносного вращения, то направление кориолисова ускорения 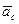 определяется поворотом относительной скорости точки
определяется поворотом относительной скорости точки 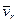 на угол 90° в сторону вращения диска.
на угол 90° в сторону вращения диска.
Из четырех составляющих ускорений три направлены по одной прямой. При этом  и
и  , т. е.
, т. е. 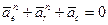 .
.
Поэтому 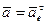 , т. е. абсолютное ускорение точки М совпадает по направлению с переносным вращательным ускорением и имеет одинаковый с ним модуль, т. е. а = 10 см/с2.
, т. е. абсолютное ускорение точки М совпадает по направлению с переносным вращательным ускорением и имеет одинаковый с ним модуль, т. е. а = 10 см/с2.
Вывод
В данной главе рассмотрены наиболее очевидные и известные параметры движения. Сделан упор на векторный характер кинематических величин: скоростей и ускорений. Показана связь между линейными и угловыми характеристиками движения. Рассмотрены сложные случаи движения точки и тела.
Контрольные вопросы
1. Дайте определение линейной и угловой скоростей.
2. Что такое линейное ускорение?
3. Как расположен вектор угловой скорости?
4. Что такое плоское движение тела?
5. Дайте определение мгновенного центра скоростей.
6. Как рассчитывается ускорение точки тела в случае его плоскопараллельного движения?
7. Опишите характеристики движений, образующих сложное движение точки.
8. Сформулируйте правило определения ускорения Кориолиса в формулировках векторного произведения и Н.Е.Жуковского.
ГЛАВА 4 ОСНОВНОЕ УРАВНЕНИЕ ДИНАМИКИ
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 4292; Нарушение авторских прав?; Мы поможем в написании вашей работы!