Кинематика твердого тела

Вопросы, связанные с движением твердого тела, помимо самостоятельного значения играют важную роль еще и в другом отношении. С твердым телом, как известно, может быть связана система отсчета, служащая для пространственно-временного описания различных движений. Поэтому изучение характера движения твердых тел равносильно по существу изучению движений соответствующих систем отсчета. Результаты, которые мы получим в этом параграфе, будут неоднократно использоваться в дальнейшем.

Различают пять видов движения твердого тела: 1) поступательное, 2) вращение вокруг неподвижной оси, 3) плоское движение, 4) сферическое движение (вокруг неподвижной точки) и 5) свободное движение. Первые два движения (поступательное и вращение вокруг неподвижной оси) являются основными движениями твердого тела. Остальные виды движения твердого тела, оказывается, можно свести к одному из основных движений или к их совокупности (это будет показано на примере плоского движения).

В данном параграфе будут рассмотрены первые три вида движения и вопрос сложения угловых скоростей.

Поступательное движение. Это такое движение твердого тела, при котором любая прямая, связанная с телом, все время остается параллельной своему начальному положению. Например, вагон, движущийся по прямому участку пути; кабина колеса обозрения и др.

При поступательном движении все точки твердого тела совершают за один и тот же промежуток времени равные по величине и направлению перемещения. Поэтому скорости и ускорения всех точек тела в данный момент времени одинаковы. Это обстоятельство позволяет свести изучение поступательного движения твердого тела к изучению движения отдельной точки тела, т. е. к задаче кинематики точки.

Таким образом, поступательное движение твердого тела может быть полностью описано, если известны зависимость от времени радиус-вектора 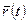любой точки этого тела и положение последнего в начальный момент.

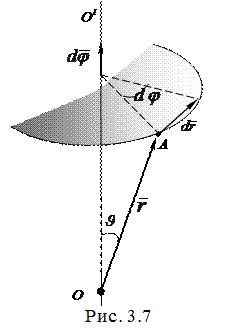
Вращение вокруг неподвижной оси. Пусть твердое тело вращается вокруг неподвижной в данной системе отсчета оси 00' (рис. 3.7). Рассмотрим бесконечно малый поворот тела вокруг этой оси. Соответствующий угол поворота будем характеризовать вектором 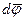, модуль которого равен углу поворота, а направление совпадает с осью 00', причем так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора 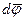(рис. 3.7).

Теперь найдем элементарное перемещение любой точки А твердого тела при таком повороте. Положение точки А зададим радиусом-вектором 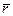, проведенным из точки О на оси вращения. Тогда линейное перемещение конца радиус-вектора 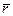связано с углом поворота соотношением (см. рис. 3.7)

,

или в векторном виде

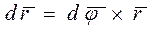(3.11)

Здесь важно отметить, что это равенство справедливо лишь для бесконечно малого поворота . Другими словами, только бесконечно малые повороты можно рассматривать как векторы. Для конечного поворота на угол 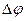линейное перемещение точки А, как следует из рис. 3.7, есть

.

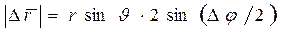Отсюда сразу видно, что перемещение нельзя представить как векторное произведение векторов и 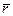. Это возможно лишь в случае бесконечно малого поворота 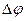, в пределах которого радиус-вектор 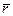можно считать неизменным.

Кроме того, можно показать, что введенный нами вектор 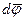удовлетворяет основному свойству векторов - векторному сложению. В самом деле, представим себе, что твердое тело совершает два элементарных поворота и 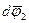вокруг разных осей, проходящих через неподвижную точку О. Тогда результирующее перемещение 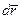произвольной точки А тела, радиус-вектор которой относительно точки О равен 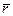, можно представить так:

, (3.12)

где 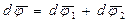, т. е. два данных поворота 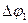и 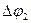эквивалентны одному повороту на угол 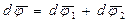вокруг оси, совпадающей с вектором 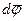и проходящей через точку О.

Заметим, что при рассмотрении таких величин, как радиус-вектор 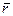, скорость , ускорение 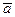не возникал вопрос о выборе их направления: оно вытекало естественным образом из природы самих величин. Подобные векторы называют полярными. В отличие от них векторы типа 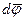, направление которых связывают с направлением вращения, называют аксиальными.

Введем теперь векторы угловой скорости и углового ускорения. Вектор угловой скорости определяют как

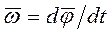, (3.13)

где dt - промежуток времени, за который тело совершает поворот .

Вектор совпадает по направлению с вектором 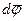и представляет собой аксиальный вектор.

Изменение вектора со временем характеризуют вектором углового ускорения 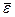, который определяют как

(3.14)

Направление вектора совпадает с направлением - приращения вектора . Вектор , как и , является аксиальным.

Запишем выражения для угловой скорости и углового ускорения в проекциях на ось вращения Z, положительное направление которой свяжем с положительным направлением отсчета координаты φ - угла поворота – правилом правого винта (рис. 3.8). Тогда проекции и векторов и 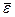на ось Z, будут определяться следующими формулами:

, (3.15)

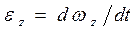(3.16)

Здесь и - величины алгебраические. Их знак характеризует направление соответствующего вектора. Например, если > 0, то направление вектора совпадает с положительным направлением оси Z; если же < 0, то направление вектора противоположно. Аналогично и для углового ускорения.

Таким образом, зная зависимость - закон вращения тела, по формулам (3.15) и (3.16) можно найти как угловую скорость, так и угловое ускорение в каждый момент времени. И наоборот, зная зависимость углового ускорения от времени и начальные условия, т. е. угловую скорость 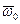и угол в начальный момент времени, можно найти как , так и .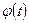

Представление угловой скорости и углового ускорения в виде векторов оказывается чрезвычайно плодотворным, особенно при изучении более сложных движений твердого тела. Это дает возможность во многих случаях получить большой выигрыш в наглядности, а также резко упростить как анализ движения, так и соответствующие расчеты.

Задача 3.4

Твердое тело вращается вокруг неподвижной оси по закону φ = bt - ct²/2, где b и c - некоторые положительные постоянные. Найти характер движения этого тела.

Согласно (3.15) и (3.16),

= b — ct; = - с = const.

Отсюда видно, что тело, вращаясь равномерно замедленно ( < 0), останавливается в момент t₀ = b / c, а затем направление вращения (знак ) изменяется на противоположное (рис. 3.9).

Отметим, что решение всех задач на вращение твердого тела вокруг неподвижной оси аналогично по форме задачам на прямолинейное движение точки. Достаточно заменить линейные величины х, v_x и а_x на соответствующие угловые φ, ω_z, и ε_z, и мы получим аналогичные закономерности и соотношения для вращающегося тела.

Связь между линейными и угловыми величинами. Найдем скорость 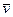произвольной точки А твердого тела, которое вращается вокруг неподвижной оси с угловой скоростью . Пусть положение точки А относительно некоторой точки О оси вращения характеризуется радиусом-вектором 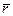(рис.3.10). Воспользуемся формулой (3.11), поделив ее на соответствующий промежуток времени dt. Так как и , то

, (3.17)

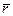т. е. скорость v любой точки А твердого тела, вращающегося вокруг некоторой оси с угловой скоростью , равна векторному произведению на радиус-вектор точки А относительно произвольной точки О оси вращения (см. рис. 3.10).

Модуль вектора (3.17)

v = ω r sinυ = ω ρ,

где ρ — радиус окружности, по которой движется точка А.

Таким образом,

v = ωρ.

Продифференцировав (3.17) по времени, найдем ускорение 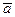точки А:

,

или

. (3.18)

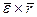В данном случае (ось вращения неподвижна) , поэтому вектор представляет собой тангенциальное ускорение (вращательное). Вектор же - это нормальное ускорение 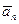(центростремительное). Модули этих ускорений равны:

; .

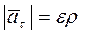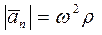Отсюда модуль полного ускорения 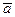есть

.

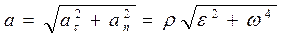Задача 3.5

Точка А движется по дуге окружности радиусом ρ (рис. 3.11). Ее скорость зависит от дуговой координаты s по закону 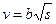, где b - постоянная. Найти зависимость от s угла α между вектором полного ускорения и вектором скорости точки.

Из рис 3.11 видно, что угол α можно определить по формуле . Найдем: a_n и а_τ:

Отсюда: tgα = 2s/ρ.

Плоское движение твердого тела. Это такое движение, при котором каждая точка твердого тела движется в плоскости, параллельной некоторой неподвижной (в данной системе отсчета) плоскости. При этом плоская фигура Ф, образованная сечением тела этой неподвижной плоскостью Р (рис. 3.12), в процессе движения все время остается в этой плоскости; например цилиндр, катящийся по плоскости без скольжения. Нетрудно сообразить, что положение твердого тела при плоском движении однозначно определяется положением плоской фигуры Ф в неподвижной плоскости Р. Это позволяет свести изучение плоского движения твердого тела к изучению движения плоской фигуры в ее плоскости.

Пусть плоская фигура Ф движется в своей плоскости Р, неподвижной в К - системе отсчета (рис. 3.13). Положение фигуры Ф на плоскости можно определить, задав радиус-вектор произвольной точки О¹ фигуры и угол φ

между радиус-вектором 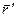, жестко связанным с фигурой, и некоторым фиксированным направлением в K - системе отсчета. Тогда плоское движение твердого тела будет описываться двумя уравнениями:

; φ = φ (t).

Ясно, что если за промежуток времени dt радиус-вектор точки А (см. рис. 3.13) повернется на угол dφ, то на такой же угол повернется и любой отрезок, связанный с фигурой. Другими словами, поворот фигуры на угол dφ не зависит от выбора точки О'. А это значит, что и угловая скорость фигуры тоже не зависит от выбора точки О', и мы имеем право называть угловой скоростью твердого тела как такового.

Найдем теперь скорость 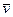произвольной точки А тела при плоском движении. Введем вспомогательную K' систему отсчета, которая жестко связана с точкой О' тела и перемещается поступательно относительно K -системы (см. рис. 3.13). Тогда элементарное перемещение 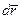точки А в K - системе можно записать в виде

,

где - перемещение K' - системы (точки О'), a - перемещение точки А относительно K' - системы.

Перемещение обусловлено вращением тела вокруг неподвижной в K' - системе оси, проходящей через точку О'; согласно (3.11) 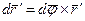. Подставив это выражение в предыдущее и поделив обе части полученного равенства на dt, найдем*

, (3.19)

т. е. скорость любой точки А твердого тела при плоском движении складывается из скорости произвольной точки О' этого тела и скорости , обусловленной вращением тела вокруг оси, проходящей через точку О'. Подчеркнем еще раз, что 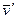- это скорость точки А относительно поступательно движущейся K' - системы отсчета, жестко связанной с точкой О'.

Иначе говоря, плоское движение твердого тела можно представить как совокупность двух основных видов движения - поступательного (вместе с произвольной точкой О' тела) и вращательного (вокруг оси, проходящей через точку О').

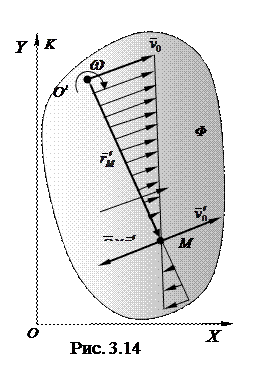
Теперь покажем, что плоское движение можно свести к чисто вращательному. Действительно, при плоском движении скорость произвольной точки О' тела перпендикулярна к вектору , а это значит, что всегда можно найти такую точку М, жестко связанную с телом (точка М может оказаться и вне тела), скорость которой в данный момент времени. Из условия 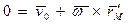можно найти положение точки М, т. е. ее радиус-вектор относительно точки О' (рис. 3.14) Этот вектор перпендикулярен к векторам и , его направление соответствует векторному произведению , а модуль .

___________________________

*Заметим, что формула (3.19) оказывается справедливой и для любого сложного движения твердого тела.

Точка М определяет и положение соответствующей оси (она совпадает по направлению с вектором ). Движение твердого тела в данный момент времени представляет собой чистое вращение вокруг этой оси. Такую ось называют мгновенной осью вращения.

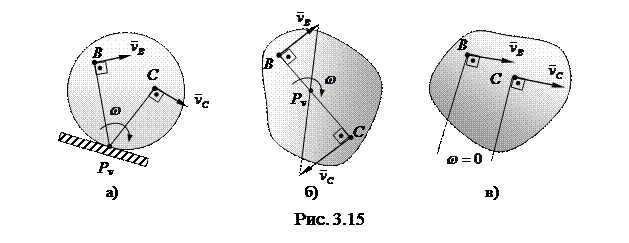
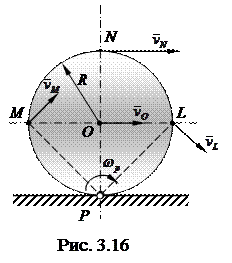
Положение мгновенной оси, вообще говоря, меняется со временем

рис.3.15 а), б), в). Например, в случае катящегося по плоскости цилиндра

мгновенная ось в каждый момент времени совпадает с линией касания

цилиндра с плоскостью (рис. 3.15 а) точка Р_v.

Задача 3.6

Колесо радиусом R (рис. 3.16) катится без скольжения по неподвижной прямой, имея скорость центра v ₀ Определить скорости точек М, N и L обода колеса в данный момент времени.

Решение. Мгновенная ось вращения в рассматриваемой задаче находится в точке Р соприкосновения колеса с прямой. Угловая скорость колеса определится из формулы

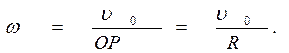
Скорости указанных в условии точек определяем по формуле:

v_N = ω * PN = ω * 2 R = 2 v₀;

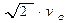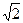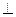v_M = v_L = ω * МР = , т. к. MP = LP = R ; v_N NP,

v_M 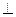МР и v_L 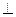LP.

Сложение угловых скоростей. Рассмотрим движение твердого тела, вращающегося одновременно вокруг двух пересекающихся осей. Сообщим некоторому телу вращение с угловой скоростью вокруг оси ОА (рис. 3.17) изатем эту ось приведем во вращение с угловой скоростью вокруг оси ОВ, неподвижной в K - системе отсчета. Найдем результирующее движение тела в K - системе. Введем вспомогательную K' - систему отсчета, жестко связанную с осями ОА и ОВ. Ясно, что эта система вращается с угловой скоростью 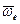, и тело вращается относительно нее с угловой скоростью .

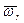За промежуток времени dt тело совершит поворот 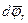вокруг оси ОА в K' - системе и одновременно поворот 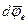вокруг оси ОВ вместе с K' - системой. Суммарный поворот согласно (3.12) есть . Поделив обе части этого равенства на dt, получим

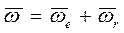. (3.20)

Таким образом, результирующее движение твердого тела в K - системе представляет собой чистое вращение с угловой скоростью вокруг оси OΩ, совпадающей в каждый момент с вектором и проходящей через точку О (см. рис. 3,17). Эта ось OΩ перемещается относительно K - системы - она поворачивается с угловой скоростью вместе с осью ОА вокруг оси ОВ – называется мгновенной осью вращения

Нетрудно сообразить, что даже в том случае, когда угловые скорости и 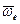не меняются по модулю, тело будет обладать в K - системе угловым ускорением, вектор 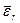которого согласно (3.14) направлен за плоскость рис. 3.17. Рассмотрим это подробно на примере на примере 1.7

Задача 3.7

Круглый конус с радиусом основания r и высотой h катится без скольжения по поверхности стола, как показано на рис. 3.18 Вершина конуса закреплена шарнирно в точке О на уровне точки С — центра основания конуса. Точка С движется с постоянной скоростью v. Найти:

1) угловую скорость и

2) угловое ускорение 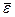конуса относительно стола.

Решение. 1. Согласно (3.20)

,

где 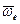и - угловые скорости вращения вокруг осей 00' и ОС соответственно.

Модули векторов 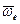и легко найти с помощью рис. 3.18:

.

Их отношение 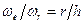. Отсюда следует, что вектор совпадает в каждый момент времени с образующей конуса, которая проходит через точку касания А.

Модуль вектора и есть

.

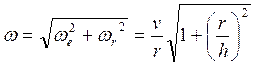2. Угловое ускорение ε конуса согласно (1.14) есть производная вектора по времени. Так как вектор 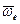= const, то

.

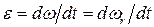Вектор , оставаясь постоянным по модулю, поворачивается вокруг оси 00' с угловой скоростью 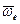. Его приращение за промежуток времени dt равно по модулю 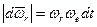, или в векторном виде . Таким образом,

.

Модуль этого вектора ε = v²/rh.

И последнее замечание. Тот факт, что вектор угловой скорости удовлетворяет основному свойству векторов - векторному сложению, в свою очередь позволяет представить как векторную сумму составляющих на определенные направления, т. е. 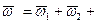..., где все векторы относятся к одной и той же системе отсчета. Этим удобным и полезным приемом часто пользуются при анализе сложного движения твердого тела.

Дата добавления: 2014-11-29