Инерциальные системы отсчета

В рамках кинематики, где речь идет лишь об описании движений и не затрагивается вопрос о причинах, вызывающих эти движения, никакой принципиальной разницы между различными системами отсчета нет, и все они в этом отношении равноправны. Совершенно иначе обстоит дело в динамике - при изучении законов движения. Здесь обнаруживается принципиальное различие между разными системами отсчета и преимущества одного класса систем отсчета по сравнению с другими.

В принципе можно взять любую из бесчисленного множества систем отсчета. Однако законы механики в разных системах отсчета имеют, вообще говоря, различный вид и может оказаться, что в произвольной системе отсчета законы даже совсем простых явлений будут выглядеть весьма сложно. Естественно, возникает задача отыскания такой системы отсчета, в которой законы механики выглядели бы возможно более просто. Такая система отсчета, очевидно, наиболее удобна для описания механических явлений.

Рассмотрим с этой целью вопрос, связанный с ускорением материальной точки относительно некоторой произвольной системы отсчета. Какова причина этого ускорения? Опыт показывает, что этой причиной может быть как действие на данную точку каких-то определенных тел, так и свойства самой системы отсчета (действительно, относительно разных систем отсчета ускорение в общем случае будет различным).

Можно, однако, предположить, что существует такая система отсчета, в которой ускорение материальной точки целиком обусловлено только взаимодействием ее с другими телами. Свободная материальная точка, не подверженная действию никаких других тел, движется относительно такой системы отсчета прямолинейно и равномерно, или, как говорят, по инерции. Такую систему отсчета называют инерциальной.

Утверждение, что инерциальные системы отсчета существуют, составляет содержание первого закона классической механики - закона инерции Галилея - Ньютона.

Существование инерциальных систем отсчета подтверждается опытом. Первоначальными опытами было установлено, что такой системой отсчета является Земля. Последующие более точные опыты (опыт Фуко и все аналогичные ему) показали, что эта система отсчета не совсем инерциальная. А именно: были обнаружены ускорения, существование которых нельзя объяснить действием каких-либо определенных тел.

Системы отсчета, движущиеся с ускорением относительно инерциальных систем, называют неинерциальными.

Важной особенностью инерциальных систем отсчета является то, что по отношению к ним пространство и время обладают определенными свойствами симметрии. А именно: опыт убеждает, что в этих системах отсчета время однородно, а пространство однородно и изотропно.

Однородность времени заключается в том, что протекание физических явлений (в одних и тех же условиях) в разное время их наблюдения одинаково. Иначе говоря, различные моменты времени эквивалентны друг другу по своим физическим свойствам.

Однородность и изотропность пространства заключается в том, что свойства пространства одинаковы в различных точках (однородность), а в каждой точке одинаковы во всех направлениях (изотропность).

Принцип относительности Галилея. Для инерциальных систем отсчета справедлив принцип относительности, согласно которому все инерциальные системы по своим механическим свойствам эквивалентны друг другу. Это значит, что никакими механическими опытами, проводимыми «внутри» данной инерциальной системы, нельзя установить, покоится эта система отсчета или движется. Во всех инерциальных системах отсчета свойства пространства и времени одинаковы, одинаковы также и все законы механики.

Это утверждение составляет содержание принципа относительности Галилея - одного из важнейших принципов классической механики. Этот принцип является обобщением опыта и подтверждается всем многообразием приложений классической механики к движению тел, скорости которых значительно меньше скорости света.

Все сказанное достаточно ясно свидетельствует об исключительности свойств инерциальных систем отсчета, в силу которых именно эти системы, должны, как правило, использоваться при изучении механических явлений.

Найдем формулы преобразования координат при переходе от одной инерциальной системы отсчета к другой. Пусть инерциальная система K' движется со скоростью 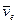- относительно другой инерциальной системы K. Выберем оси координат X', Y', Z' - K' - системы параллельно соответствующим осям X, Y, Z - K - системы, причем так, чтобы оси X' и X совпадали между собой и были направлены вдоль вектора 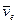(рис. 4.1). Взяв за начало отсчета времени момент, когда начала координат О' и О совпадали, запишем связь между радиусами-векторам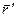и и 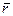одной и той же точки А в K' и K системах:

(4.1)

и, кроме того,

. (4.2)

Здесь подразумевается, что длины отрезков и ход времени не зависят от состояния движения и, следовательно, одинаковы в обеих системах отсчета. Предположение об абсолютности пространства и времени лежит в самой основе представлений классической механики, представлений, основанных на обширном экспериментальном материале, относящемся к изучению движений со скоростями, значительно меньшими скорости света.

Соотношения (4.1) и (4.2) представляют собой так называемые преобразования Галилея. В координатах эти преобразования имеют вид:

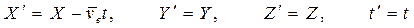. (4.3)

Продифференцировав (4.1) по времени найдем классический закон преобразования скорости точки при переходе от одной инерциальной системы отсчета к другой:

. (4.4)

Дифференцируя это выражение по времени с учетом того, что 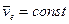, получаем 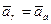, т. е. ускорение точки действительно одно и то же во всех инерциальных системах отсчета.

Дата добавления: 2014-11-29