Методы расчета усилий в стержнях ферм

Фермой называют плоскую или пространственную конструкцию, составленную из стержней, соединенных между собой шарнирами, и служащая для восприятия внешних нагрузок и передачи их на опоры. 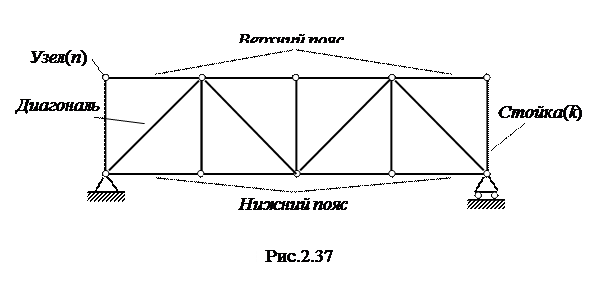Точка, где стержни соединяются шарнирами, называется узлом. Нижняя часть фермы называется нижним поясом, а верхняя часть – верхним поясом (рис.2.37). Вертикальные стержни называются стойками, а наклонные – диагоналями (при наличии стоек) или раскосами. По определению, ферма должна обеспечивать неизменяемость ее формы (жесткость).

Первый шаг при расчете фермы - определение сил, возникающих в ее стержнях. В задачах статики предполагают, что по концам стержней расположены шарниры, цилиндрические или сферические. Это позволяет считать, что силы всегда направлены вдоль стержней.

Рассмотрим два метода расчета ферм.

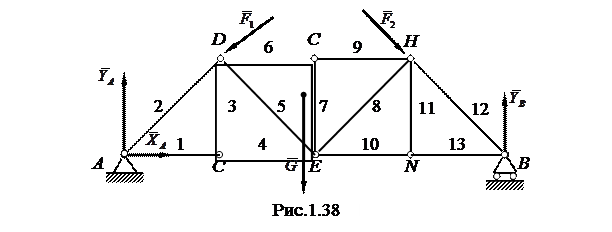Метод вырезания узлов. При расчете ферм вначале составляют уравнения равновесия для фермы в целом и определяют неизвестные опорные реакции. Для плоской фермы, показанной на рис. (2.38) - это

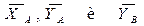, поскольку в общем случае система сил, действующая на нее, - плоская произвольная. Все углы между смежными стержнями фермы считают известными.

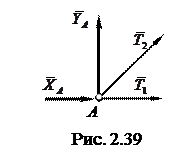После определения реакций выделяют узел, котором сходятся два стержня, например А (рис. 2.39). Силы 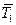и , действующие со стороны стержней на узел А, направляют вдоль стержня в ту или иную сторону. Полученный при решении отрицательный знак будет свидетельствовать о том, что истинное направление силы обратно выбранному. Для узла А составляют два уравнения равновесия, из которых определяют силы 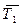и .

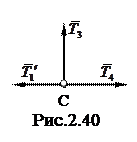Затем выделяют узел С, в котором сходятся стержни 1, 3 и 4 (см. рис. 2.40). Силы в двух последних стержнях подлежат определению. К узлу прикладывают силу 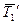(рис. 2.40), которая согласно аксиоме 4 равна силе 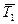по величине, но противоположна по направлению. Вновь составляют два уравнения равновесия, из которых находят силы 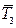и 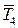. Необходимо иметь в виду, что силы 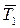, , 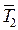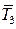и 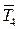- это силы, с которыми стержни действуют на узел. Силы действия узла на стержни обратные по направлению.

Следующим выделяемым узлом будет тот, в котором, сходятся стержни 2, 3, 5 и 6 (см. рис. 2.41). Неизвестны силы 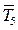и 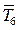и т. д.

К началу расчета последнего узла В силы 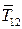и 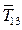будут уже определены из рассмотрения предыдущих узлов. Поэтому уравнения равновесия для этого узла удовлетворяются тождественно и служат для проверки правильности расчетов.

Аналогичный метод применяют и при расчете пространственной простой фермы с тем отличием, что для каждого узла составляют три уравнения равновесия пространственных систем сходящихся сил.

Метод сечений (метод Риттера). Вначале, как и при расчете, способом вырезания узлов, рассматривая равновесие фермы в целом, определяют реакции опор 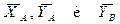. Затем разделяют ферму сечением, проходящим через три стержня, силы в которых подлежат определению. Отбрасывая одну часть фермы, действие ее на рассматриваемую часть заменяют силами, направленными вдоль стержней от узлов D и С (рис. 2.41). Составляют уравнения равновесия для плоской системы произвольно расположенных

сил, откуда определяют искомые силы, например 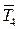, 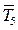и .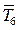

Задача 2.7

В мостовой ферме, изображенной на рис. 2.48, узлы С, D и Е загружены одинаковой нагрузкой Р. Раскосы составляют углы 45° с горизонтом. Найти усилия в стержнях 1, 2, 3 и 4, вызываемые данной нагрузкой.

Решение. В силу симметрии фермы и нагрузки заключаем, что опорные реакции R_A и R_B равны между собой и составляют по половинке всей внешней нагрузки:

R_A = R_B = 3 P /2.

Проведем сквозное сечение 1-1 и рассмотрим равновесие правой части фермы. Принимая за моментную точку Е, можем записать:

∑М_Е = 0: N₁ a + R_B а = 0,

т.е. N₁. = - R_B = - 3 P/2.

Принимая за моментную точку Н, аналогично получим:

∑ М_H = 0: - N ₃ a – Р а + R_B 2 а = 0,

откуда N ₃ = 2 Р.

Составим теперь для правой части фермы уравнение равновесия в виде равенства нулю суммы проекций всех сил на ось Y:

∑Y = 0: N ₂ cos 45⁰ - P + R_B = 0;

найдём:

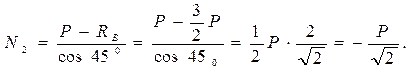
Для определения усилия в стойке 4 рассмотрим равновесие узла D. Составляя уравнение проекции сил, сходящихся в узле D, на ось Y, получим N ₄ = P. Задача решена.

2.13. Центр параллельных сил

Под системой параллельных сил понимают совокупность сил, линии, действия которых параллельны между собой (рис. 2.49). Выберем в качестве центра приведения начало системы координат О, ось Z которой направим параллельно линиям действия сил. В результате приведения получим главный вектор 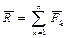, направленный по оси Z, и главный момент 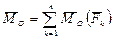. Вектор главного момента 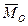лежит в плоскости Оxy, так как вектор момента каждой силы относительно точки О перпендикулярен к плоскости, проходящей через эту точку и линию действия силы, и, следовательно, расположен в плоскости ОXY. Таким образом, главный вектор и главный момент взаимно перпендикулярны.

Частными случаями приведения являются следующие.

1. Если для данной системы сил 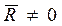, 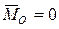то система сил приводится к равнодействующей, имеющей своей линией действия ось Z.

2.Если для данной системы сил 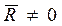, 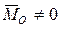но 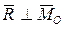, то и в этом случае система сил приводится к равнодействующей 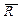, однако последняя отстоит от центра приведения на расстояние d = M_О / R.

3. Если , , 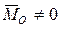то система сил приводится к паре сил.

4. Если , , 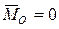то система сил уравновешенна.

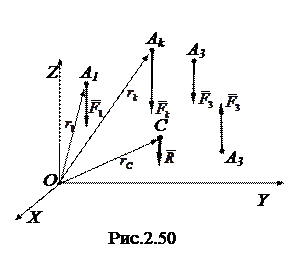Главный вектор и главный момент взаимно перпендикулярны независимо от выбора центра приведения, поэтому систему параллельных сил невозможно привести к динаме, т. е. к случаю, когда оба эти вектора направлены по одной прямой. В дальнейшем будем рассматривать лишь случаи, когда система параллельных сил приводится к равнодействующей.

Будем считать каждую силу системы приложенной к некоторой точке пространства, А₁,А₂, А₃ и.т. д. (рис. 2.50). Получим формулы, позволяющие по координатам точек приложения и модулям сил определить координаты центра параллельных сил С. Обратимся к рис. 2.50.

Направим ось Z параллельно линиям действия сил. Проведем из начала координат О в точки приложения каждой силы, а также равнодействующей радиус-векторы 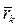, где k - 1,2, 3,..., n, и 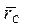. Воспользуемся теоремой Вариньона:

,

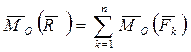или

.

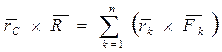Запишем каждую силу как 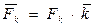, 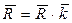где 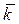- орт оси. Имеем

.

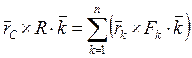Воспользуемся тем, что скалярный множитель в векторном произведении можно переносить от одного сомножителя к другому. Тогда равенство примет вид

.

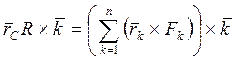В правой части равенства общий множитель - орт 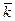- вынесен за знак суммы. Так как 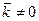, то на него можно сократить. Из полученного равенства находим радиус-вектор центра параллельных сил

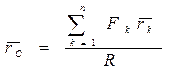, (2.62)

где .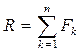

Проецируя равенство (2.62) на оси координат, получим формулы координат центра параллельных сил

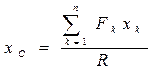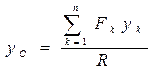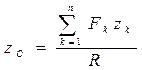; ; (2.63)

В полученных формулах как координаты точек, так и силы имеют алгебраическое значение.

Дата добавления: 2014-11-29