Основная теорема статики

Пусть дана система сил , как угодно расположенных в пространстве. По определению (2.4) геометрическая сумма системы сил

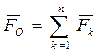
называется ее главным вектором. Векторную сумму моментов этих сил относительно какого-нибудь полюса О (центра приведения) называют главным моментом системы сил относительно этого полюса:

.

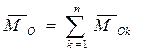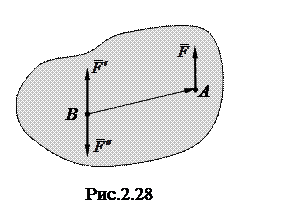
Рассмотрим некоторое твердое тело, в точке А которого приложена сила (рис. 2.28). Приложим в произвольной точке В тела систему двух сил 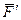и 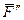, эквивалентную нулю, причем 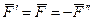. Система сил 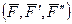эквивалентна силе и паре 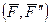с моментом:

.

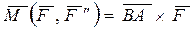Но векторное произведение 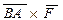выражает момент силы относительно точки В, т.е.

.

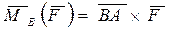Таким образом, силу, приложенную в какой-либо точке твердого тела, можно переносить параллельно самой себе в любую другую точку этого тела, добавляя при этом пару, момент которой равен моменту данной силы относительно новой точки приложения.

Назовем это предложение леммой о параллельном переносе силы. Имея это в виду, докажем теперь следующее.

Теорема. Всякая система сил эквивалентна главному вектору системы, приложенному в какой-либо точке тела (центре приведения) и главному моменту всех сил относительно этой точки.

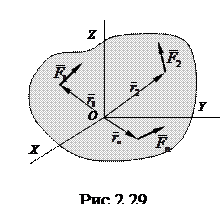Пусть на некоторое твердое тело действует произвольная пространственная система n сил . Выберем некоторый центр приведения О (рис. 2.29) и совместим его с началом прямоугольной системы координат OXZY.

Радиус-векторы точек приложения сил обозначим через , а моменты сил относительно точки О соответственно через 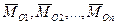, причем на основании формулы (2.16)

, , …., .

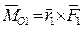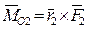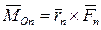Выполним параллельный перенос сил в центр приведения и сложим эти силы как сходящиеся. Применяя правило сложения сходящихся сил (2.4), получим одну силу:

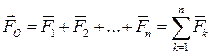(2.40)

которая по определению равна главному вектору исходной системы сил . На основании леммы о параллельном переносе силы при последовательном переносе сил в центр приведения мы должны добавлять каждый раз соответствующую пару с моментом 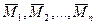. По теореме об эквивалентности пар (2.38) момент результирующей пары будет:

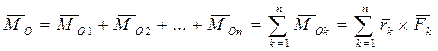. (2.41)

Но по определению есть главный момент системы сил относительно центра О, и теорема доказана.

При координатном задании сил 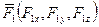, ,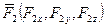…, 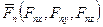главный вектор системы определим по формулам (2.7) — (2.13). Проекции главного вектора на оси координат будут:

;

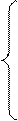
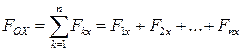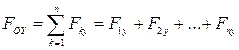; (2.42)

.

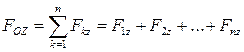Модуль главного вектора равен:

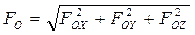, (2.43)

а его направляющие косинусы определяются формулами:

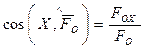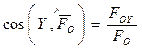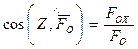, , . (2.44)

Для проекций главного момента по формулам (2.16) - (2.21) имеем:

,

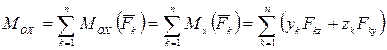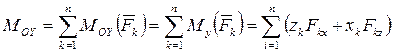, (2.45)

.

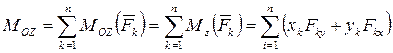Тогда модуль и направляющие косинусы главного момента определяются формулами:

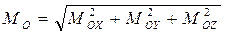; (2.46)

, , .

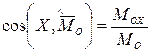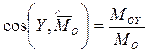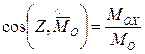Дата добавления: 2014-11-29