Система двух параллельных сил

И оси

Моменты силы относительно центра

Для рассмотрения различных систем сил необходимо ввести понятия алгебраического и векторного моментов силы относительно центра и момента относительно оси. Рассмотрим действия этих силовых факторов на твердое тело и их свойства.

Момент силы относительно центра. При рассмотрении плоской системы сил, приложенных к твердому телу, используется понятие алгебраического момента силы, относительно центра О. Под которым понимают, произведение силы на длину перпендикуляра, опущенного из центра на линию действия силы (рис. 2.17):

(2.15)

Алгебраический момент силы относительно центра О характеризует вращательный эффект силы относительно этого центра. Знак «плюс» берут в случае, когда сила 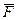стремится вращать тело против часовой стрелки, а «минус» - по часовой. Перпендикуляр h называют плечом действия силы относительно центра О. Согласно выражению (2.15) размерность момента силы - Н • м. Модуль момента силы равен удвоенной площади треугольника ОАВ:

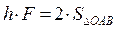, (2.15а)

и не меняется при переносе силы вдоль линии ее действия, так как при этом сохраняются основание треугольника АВ и его высота h.

Плоскость, определяемая треугольником ОАВ, - это плоскость действия момента силы.

В механике момент силы относительно центра принято изображать в виде вектора - называемого вектором момента силы относительно

центра. Этот вектор (рис. 2.18) направлен перпендикулярно к плоскости АОВ в ту сторону, откуда видно стремление силы 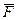повернуть плоскость АОВ, связанную с телом, против часовой стрелки. Проведем из центра О в начало вектора силы 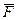радиус-вектор 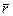и рассмотрим векторное произведение 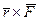. По модулю

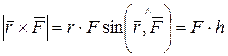, что совпадает с модулем момента силы (2.15). Направление вектора 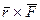совпадает с направлением вектора момента силы 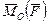. Отсюда вытекает, что вектор момента силы 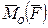совпадает с векторным произведением :

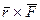. (2.16)

Пусть радиус-вектор и сила 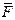заданы своими проекциями на оси: и . Тогда выражение (2.16) можно записать как:

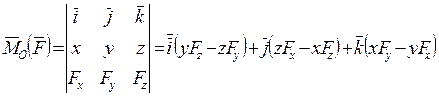(2.17)

С другой стороны, вектор можно спроецировать на оси координат:

(2.18)

Сопоставляя выражения (6.3) и (6.4), получим, что проекции вектора момента силы на оси координат можно вычислить по формулам:

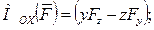
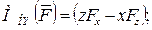
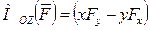. (2.19)

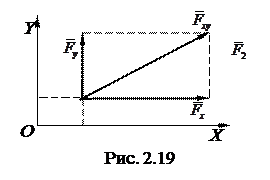
Для наглядности посмотрим, например, на систему координат со стороны оси Z (рис. 2.19). Ось Z направлена к читателю, - проекция силы на плоскость ОXY. Видно, что 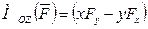. Аналогично можно рассмотреть 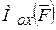и 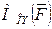. Исходя из разложения вектора момента силы в соответствии с выражением (2.18), по формулам векторной алгебры можно подсчитать его модуль:

,

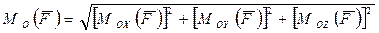или

, (2.20)

а также направляющие косинусы:

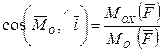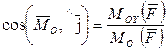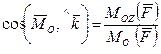; ; . (2.21)

Момент силы относительно оси. Алгебраическим моментом силы 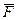относительно оси Z называют алгебраический момент проекции F_n этой силы на плоскость П (рис. 2.20), перпендикулярную к оси Z, относительно точки О пересечения оси Z с плоскостью П:

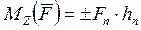(2.22)

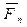Действительно, разложим силу на составляющие перпендикулярную оси Z, и 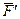, параллельную оси z (и, следовательно, перпендикулярную к плоскости П). Очевидно, что составляющая не стремится повернуть тело вокруг оси Z. Это может осуществить только составляющая .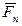

Момент силы относительно оси равен нулю, если сила 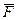и ось Z лежат в одной плоскости. При этом сила 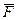либо пересекает ось и h = 0, либо параллельна ей.

Векторный момент силы (вектор момента силы) относительно оси направлен по оси в сторону, откуда действие момента 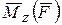видно против хода часовой стрелки. Его векторное выражение

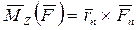(2.23)

Ранее было показано, что вектор момента силы 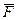относительно точки О перпендикулярен к плоскости треугольника ОАВ и по модулю равен удвоенной площади этого треугольника. Вектор момента перпендикулярен к плоскости треугольника ОА₁В₁ и также равен удвоенной его площади согласно выражению (6.1а). Но треугольник ОА₁В₁ — проекция треугольника ОАВ на плоскость П.

Следовательно, между площадями этих треугольников имеется следующая зависимость:

где γ - угол между плоскостями треугольников.

Угол γ равен также углу между перпендикулярами к плоскостям треугольников, а значит, и между векторам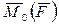и и . Таким образом, между этими векторами имеет место зависимость

, (2.24)

т. е. проекция вектора момента силы относительно некоторой точки О на ось, проходящую через эту точку, равна моменту силы относительно этой оси. Точка О на оси Z взята произвольно, и при любом ее положении проекция треугольника ОАВ на плоскость П равна треугольнику ОА₁В₁. Очевидно, что для силы, расположенной в плоскости П, угол γ = 0 и . При замене оси Z на оси X и Y, также проходящие через точку О, все приведенные ранее рассуждения остаются справедливыми. Отсюда следует, что на основании формул (2.19) и (2.24) имеют место соотношения:

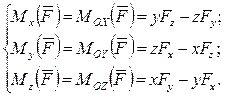(2.25)

т. е. проекции момента силы относительно центра О на оси декартовой прямоугольной системы координат равны моментам силы относительно координатных осей.

Главный момент системы сил относительно центра и оси. Пусть на тело действует система сил 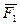, ,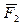… 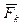. Выберем некоторый центр О и покажем момент каждой силы относительно него в виде вектора . Получим систему векторов (где k = 1,2,..., п), приложенных к точке О (рис. 2.21). Эту систему векторов можно сложить по правилу параллелограмма или многоугольника и получить результирующий вектор , который называют главным моментом системы сил относительно центра О

. (2.26)

Главный момент выражается через проекции точек приложения сил x_k, y_k, z_k и проекции сил на оси координат F_kx., F_ky, F_kz следующим образом:

(2.27)

Главный момент как вектор может быть спроецирован на какую-либо ось, например Z. При этом, как для любой результирующей, проекция ее на ось равна алгебраической сумме проекций составляющих на ту же ось:

.

Если силы лежат в одной плоскости, то векторы моментов этих сил перпендикулярны к этой плоскости и главный момент сил относительно некоторого центра О, расположенного также на плоскости, равен алгебраической сумме моментов сил относительно этого центра:

.

Следовательно, тело находится в равновесии (не вращается относительно данного центра), если главный момент сил относительно этого центра равен нулю:

(2.28)

Это векторное условие равновесия тела, стремящегося повернуться вокруг центра О (т. е. в центре О тела имеется сферический шарнир).

Исходя из векторного условия и выражения (2.27), получим скалярные условия равновесия тела:

(2.29)

Следовательно, тело находится в равновесии, если суммы моментов сил относительно координатных осей равны нулю.

Для равновесия тела относительно какой-либо одной оси необходимо, чтобы сумма моментов сил относительно этой оси равнялась нулю, например,

.

Задача 2.4

Водонапорная башня, свободно стоящая на поверхности, подвержена ветровой нагрузке, результирующая которой приложена на высоте h (рис. 2.22). Сила тяжести башни . Определить значение силы 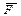, при котором башня опрокинется.

Решение. Сила стремится опрокинуть башню, повернув ее вокруг точки В. Составим сумму моментов сил относительно этой точки:

,

откуда

.

По условиям рассмотренного примера момент

М _опр = Fh называют опрокидывающим,

а момент

М_уд = GL/2 — удерживающим.

Отношение удерживающего момента к опрокидывающему называют коэффициентом устойчивости:

k _уст = М_уд / М _опр.

Для устойчивого состояния объекта необходимо, чтобы выполнялось неравенство kуст > 1, и при проектировании незакрепленных объектов выбором значения k _уст обеспечивается определенный запас их устойчивости.

Приведение двух параллельных сил, у которых линии действия параллельны, к одной силе – равнодействующей, или сложение этих сил, позволяет получить способ приведение любой системы параллельных сил к простейшему виду. Кроме того, сложение двух равных по величине, но противоположных сил приводит к введению понятия пары сил.

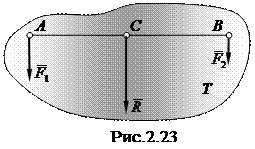Параллельные силы, направленные в одну сторону. Пусть к твердому телу Т приложены две параллельные силы 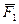и 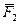направленные в одну сторону (рис.2.23). Равнодействующая таких сил, очевидно, будет иметь такое же направление, а её величина:

(2.30)

Точку С приложения равнодействующей 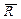можно определить если составить уравнение моментов:

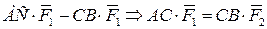(2.31)

Разделим полученное уравнение на постоянный множитель 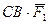, в результате получим следующее соотношение:

или .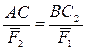

Образовав производную пропорцию, окончательно получим:

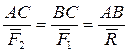. (2.32)

Таким образом, две параллельные силы, направленные в одну сторону, имеют равнодействующую силу, параллельную им, равную по величине их сумме и направленную в ту же сторону. Линия действия равнодействующей силы расположена межу линиями действия заданных сил и делит отрезок прямой между линиями действия этих сил на части, обратно пропорциональные силам внутренним образом.

Если две параллельные силы, направленные в одну сторону можно заменить одной равнодействующей, то и обратно, любую силу можно разложить на две параллельные силы, направленные в одну сторону.

Применяя последовательно правило приведения двух параллельных сил, направленных в одну сторону, к любой системе параллельных сил, направленных в одну сторону, можно привести её к одной равнодействующей силе.

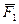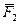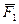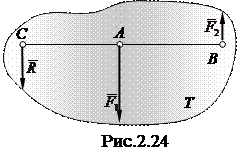
Параллельные силы, направленные в противоположные стороны. Пусть к твердому телу Т приложены две параллельные силы и , причем сила больше силы 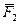(рис.2.24). Очевидно, равнодействующая будет определена как

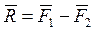, (2.33)

а точку её приложения определим как центр суммы моментов от сил 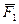и 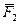по (2.32)

. (2.34)

Итак, две неравные параллельные силы, направленные в противоположные стороны, приводятся к равнодействующей силе, параллельной им, равной по величине их разности и направленной в сторону большей силы. Линия действия равнодействующей расположена за линией действия большей силы и делит отрезок прямой между линиями действия заданных сил на части, обратно пропорциональные силам внешним образом.

Если две неравные параллельные силы, направленные в противоположные стороны, можно заменить одной равнодействующей силой, то и, обратно, любую силу можно разложить на две неравные параллельные силы, направленные в противоположные стороны.

Пара сил и алгебраический момент пары сил Пару сил в механике рассматривают как одно из основных понятий наряду с понятием силы.

Парой сил называют систему двух равных по величине параллельных сил, направленных в противоположные стороны и лежащих в одной плоскости (рис 2.25).

Плоскость, в которой лежат силы, составляющие пару, называют плоскостью действия пары сил. Пара сил, приложенных к твердому телу, стремится придать ему вращательное движение (рис. 2.25).

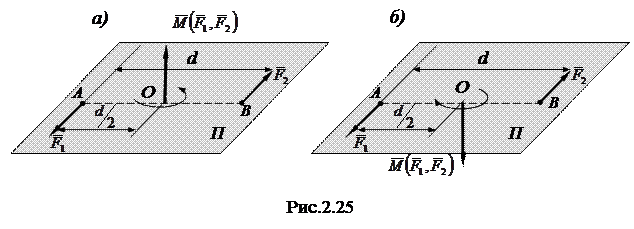
Кратчайшее расстояние d между линиями действия сил пары называют ее плечом (рис. 2.25). Механический эффект действия пары сил характеризуется ее алгебраическим моментом

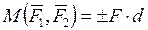(2.35)

Знак «плюс» берут в случае, если пара сил стремится вращать плоскость своего действия против часовой стрелки, а «минус» - если наоборот (рис. 2.25, а) и б)).

Векторный момент пары сил. Векторным моментом пары сил назовем вектор, величина которого равна произведению силы пары на её плечо. Векторный момент пары сил направлен перпендикулярно к плоскости действия пары сил так, чтобы конца этого вектора видеть стремление пары сил вращать тело против часовой стрелки.

Векторный момент пары сил условимся прикладывать посредине отрезка, точка О, соединяющего точки А В приложения сил (рис. 2.25). При оперировании с парами сил удобно изображать пару сил в виде одного вектора, называемого векторным моментом пары сил. Модуль векторного момента пары сил , направлен перпендикулярно к плоскости действия пары в сторону, откуда действие пары видно против часовой стрелки (рис. 2.25 а) и б)). Сам момент будет равен сумме векторных произведений:

,

но при существовании пары сил , следовательно

. (2.36)

Скалярное произведение (2.36) будет соответственно равно:

,

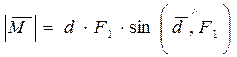следовательно, учитывая, что d есть кротчайшее расстояние между линиями действия, сил 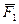и 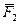при котором угол равен девяноста градусам, при котором полученное выражение соответствует (2.35).

Теорема о сумме моментов сил пары. Сумма моментов пары сил относительно любого центра равна моменту пары.

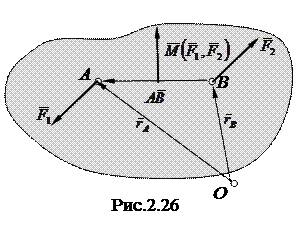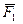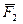Проведем из произвольно взятого центра О (рис. 2.26) радиусы-векторы точек А и В, к которым приложены силы и составляющие пару.

Тогда с учетом того, что , получим:

(2.37)

Теорема доказана.

Эта теорема имеет важное значение при решении задач, когда надо вычислять сумму моментов сил пары относительно какой – либо точки. Для этого достаточно взять момент пары сил, что справедливо для любой точки.

Две пары сил называются эквивалентными, если их действие на твердое тело одинаково при прочих условиях.

Беря во внимание доказательство теоремы о сумме моментов сил пары можно доказать следующие теоремы.

Теорема об эквивалентности двух пар сил, расположенных в одной плоскости: пару сил, действующею на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющей одинаковый с первой парой алгебраический момент.

Как следствие:

а) пару сил можно как угодно поворачивать и переносить в её плоскости действия;

б) у пары сил можно изменять плечо и силы, сохраняя, при этом алгебраический момент пары и плоскость действия.

Теорема о переносе пары сил в параллельную плоскость: действие пары сил на твердое тело не изменяется от переноса этой пары сил в параллельную плоскость.

Таким образом, условие равновесия системы пар имеет вид:

. (2.38)

Пусть две пары лежат в одной плоскости. Используя формулу, условия равновесия таких пар можно записать в виде скалярного равенства:

. (2.39)

Следовательно, для равновесия плоской системы пар необходимо и достаточно, чтобы алгебраическая сумма моментов этих пар была равна нулю.

Задача 2.5

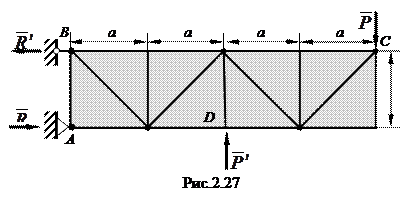
Стержневая конструкция, имеющая две шарнирные опоры А и В, нагружена парой сил (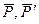), приложенных в точках С и D (рис.2.27). Пренебрегая весом конструкции, определить реакции опор. Размеры конструкции указаны на рисунке.

Решение. Активная нагрузка, действующая на конструкцию, представляет собой пару сил (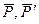). Поскольку пару можно уравновесить только парой с моментом, направленным противоположно , заключаем, что реакции опор должны образовывать пару (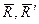), причем;

.

Записывая это равенство в виде (2.39), получим:

;

отсюда находим:

.

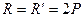Дата добавления: 2014-11-29