Условия равновесия произвольной системы сил

Пусть к твердому телу приложена произвольная система сил 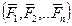. Используя основную теорему статики (2.8), приведем ее к центру О. В результате получим главный вектор и главный момент , эквивалентные исходной системе. Для равновесия этой системы необходимо и достаточно, чтобы одновременно выполнялись условия:

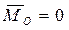, . (2.47)

Необходимость условий вытекает из того, что если какое - нибудь из них не выполняется, то исходная система приводится либо к равнодействующей (при , 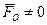), либо к паре (при , ). И в том и в другом случае система будет неуравновешенной. Вместе с тем условия (2.47) являются достаточными, поскольку при система может быть приведена только к паре , а так как , то система уравновешена.

Если ОXYZ — декартова система прямоугольных координат с началом в центре приведения О, а векторы сил и моментов заданы своими проекциями:

, ,…, ;

, ,…, ,

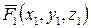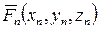то в проекциях на оси X, Y, Z уравнения равновесия принимают вид:

(2.48)

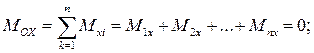
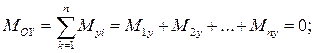(2.49)

где X₀,Y₀,Z₀ - проекции главного вектора, а М_ОX,М_ОY, М_ОZ - проекции главного момента на оси X, Y и Z.

Сделаем следующие замечания относительно условий (2.48), (2.49).

Во - первых, часть слагаемых, входящих в эти уравнения, могут представлять проекции заранее неизвестных реактивных или активных сил либо моментов. Разрешив систему уравнений (2.48), (2.49) относительно этих неизвестных, мы можем определить их значения, если только число неизвестных не превышает шести.

Во - вторых, уравнения равновесия линейны, что не создает проблем при их решении.

Для частных случаев систем сил уравнения равновесия (2.48), (2.49) упрощаются, поскольку часть их тождественно удовлетворяется. Рассмотрим эти частные случаи.

1. Пространственная система параллельных сил. Пусть все силы параллельны. Направим ось Z параллельно линиям действия сил. В этом случае проекции сил 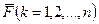на оси X и Y обращаются в нуль и первые два уравнения из группы (2.48) удовлетворяются тождественно. Таким образом, из уравнений (2.48) остается лишь одно:

. (2.50)

В уравнениях равновесия моментов (2.49) при X_i = О и Y_i = 0 последнее также удовлетворяется тождественно, поскольку проекции моментов всех сил относительно центра О на координатную ось OZ обращаются в нуль (см. (2.45)). Поэтому из уравнений группы (2.49) остаются лишь два:

,

. (2.51)

2. Плоская система параллельных сил. Уравнения равновесия для этого частичного случая вытекают из условий (2.50) и (2.51). Пусть ось Y направлена параллельно линиям действия сил (рис. 2.30). Тогда моменты всех сил относительно оси X обращаются в нуль и первое из уравнений (2.10) удовлетворяется тождественно. Следовательно, для плоской системы параллельных сил остается только два уравнения равновесия:

,

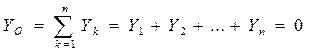. (2.52)

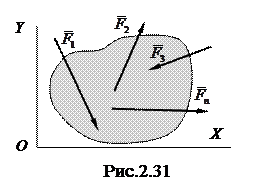3. Произвольная плоская система сил. Выберем в плоскости действия сил систему прямоугольных координат ОXY (рис. 2.31). В этом случае третье уравнение из группы (9.2) удовлетворяется тождественно, поскольку проекции всех сил системы на ось Z равны нулю .

Из второй группы уравнений равновесия (2.49) два первых уравнения равновесия также тождественно удовлетворяются, поскольку все силы лежат в одной плоскости с осями X и Y. Следовательно, условия равновесия плоской произвольной системы сил принимают вид:

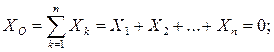
(2.53)

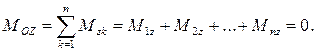
Задача 2.6

Мост состоит из двух частей, соединенных в точке С (рис.2.32). Сила, действующая на левую часть моста, , на правую - .

Определить опорные реакции в пятовых шарнирах А и В и усилия в ключевом шарнире С трех шарнирной арки моста (рис. 2.32а) под действием сил и . Размеры даны на рис. 2.32.

Решение. Берем сначала всю систему. Так как в шарнирах направления реакций заранее неизвестны, мы вводим их составляющие — горизонтальную X и вертикальную Y:

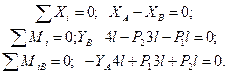
Отсюда ; .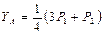

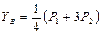Разрезаем систему по шарниру С, отбрасываем правую часть и вводим силы 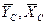(левая часть представлена отдельно, рис. 2.32,б):

Отсюда ;

Если бы мы составляли уравнения равновесия также и для правой части, то в точке С ввели бы силы 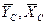, направленные противоположно соответствующим силам, действующим на левую часть.

Дата добавления: 2014-11-29