Системы сходящихся сил. Условия равновесия

Аналитический способ определения равнодействующей

Каждую силу системы сходящихся сил можно разложить на составляющие по осям прямоугольной декартовой системы координат:

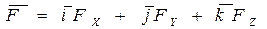, (2.7)

где 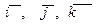- орты осей X, Y, Z.

Разложив каждую силу в формуле (2.7) и вынося орты 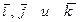за знаки сумм, получим:

(2.8)

Аналогично можно разложить и равнодействующую:

. (2.9)

Приравнивая выражения (2.9) и (2.8), получим, что

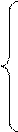
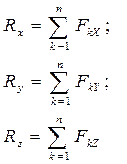. (2.10)

Определив проекции равнодействующей, можно найти ее модуль

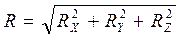, (2.11)

а также косинусы углов между вектором силы 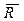и осями координат:

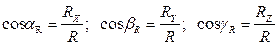. (2.12)

Эти косинусы связаны между собой соотношением

.

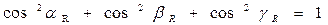Косинусы углов между некоторым вектором и осями координат называют также направляющими косинусами данного вектора.

Для системы взаимно уравновешенных сил 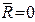, а значит, 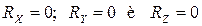, отсюда

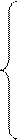
. (2.13)

Уравнения (2.13) называют уравнениями (или условиями) равновесия системы сходящихся сил в аналитической форме. Для плоской системы сходящихся сил достаточно системы координат из двух осей, например X и Y. Условия равновесия имеют вид

, (2.14)

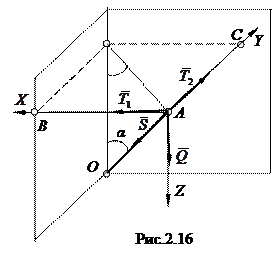
и число неизвестных сил должно быть не более двух.

Задача 2.3

Груз Q, сила тяжести которого 120Н, поддерживается в равновесии стержнем АО и цепями АВ и АС (рис. 2.16). По концам стержня имеются шарниры. Длины цепей равны, т. е. АВ=А С; угол a = 300. угол ВАС - 90⁰. Определить силы в цепях АВ и АС и стержне АО, считая их невесомыми.

Решение. Рассмотрим равновесие узла А, заменив действие стержня и цепей на узел А реакциям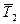и , и 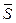, направив их, как показано на рис. 2.16. Получим систему четырех сил, сходящихся в точке А, направим оси координат вдоль цепей и нити подвеса груза. Составим уравнения равновесия, спроецировав систему сил на оси координат. При определении проекции реакции 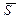на оси X и Y применим метод двойного проецирования, спроецировав ее вначале на плоскость АXY, а затем на оси X и Y.

Имеем: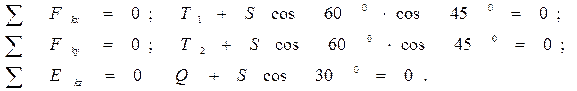

Из третьего уравнения находим, что S = - Q/cos 30 ° = - 80 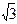H.

Знак «минус» указывает на то, что выбранное направление реакции 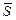следует заменить на обратное.

Из первого и второго уравнений находим

.

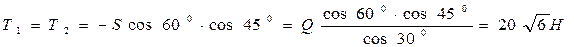Положительный знак результата свидетельствует о том, что выбранное направление реакци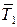й и соответствует действительному. На стержень АО и цепи действуют усилия, обратные реакциям. Следовательно, стержень АО сжат, а цепи растянуты (рис. 2.16).

Дата добавления: 2014-11-29