Аксиомы теоретической механики

Применение метода абстракций и обобщение результатов многовекового опыта, непосредственных наблюдений и производственной деятельности людей позволили установить некоторые общие законы статики. Эти законы называются аксиомами.

1. Аксиома об уравновешенности двух сил, приложенных к твердому телу: две силы, приложенные к твердому телу, взаимно уравновешиваются только в том случае, если силы направлены в разные стороны вдоль общей линии действия и модули их равны (рис.2.3 а)):

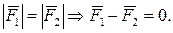
Следствие. Если система сил имеет равнодействующую, то уравновешивающая и равнодействующая силы равны по модулю, лежат на одной прямой и направлены в противоположные стороны.

2. Аксиома присоединения и исключения уравновешенных систем сил: действие системы сил на твердое тело не изменится, если к ней добавить или из нее исключить уравновешенную систему сил (рис.2.3 б)):

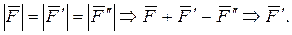
Отсюда следует, что силу, приложенную к твердому телу, можно переносить вдоль линии действия, при этом действие силы на тело не будет меняться (т.е. любая сила – это скользящий вектор).

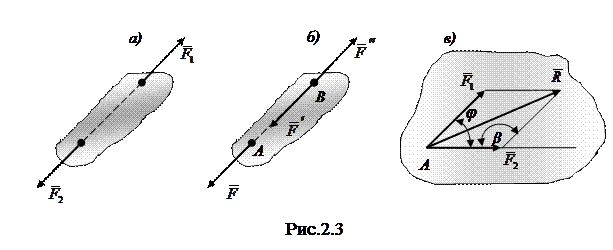
3. Аксиома параллелограмма сил. Равнодействующая двух сил с пересекающимися линиями действия приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах:

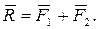
Модуль равнодействующей находится (рис.2.3 в)):

,

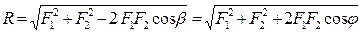так как 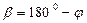, где 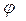- угол между силам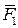и и .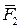

4. Аксиома равенства действия и противодействия. Два тела действуют друг на друга с силами, равными по величине и направленными по одной линии действия, но в противоположные стороны (рис. 2.4 а), б)).

Взаимодействие тел может быть как контактным, когда тела соприкасаются одно с другим (рис. 2.4 а)), так и на расстоянии, через силовые поля (рис. 2.4 б)). Необходимо иметь в виду, что силы и не составляют уравновешенной системы сил, поскольку приложены к разным телам.

5. Аксиома отвердевания. Равновесие сил, приложенных к деформируемому твердому телу, не нарушается, если тело считать абсолютно твердым.

Из этой аксиомы следует, что внешние силы, приложенные к деформируемому твердому телу, должны удовлетворять условиям равновесия, записанным в предположении недеформируемости этого тела. Однако для деформируемого тела эти условия необходимы, но не всегда достаточны.

Поясним сказанное на примере. На рис. 2.5 показана нить АВ, к которой приложены две равные и противоположно направленные силы 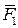и 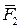. В том случае, когда приложенные силы растягивают нить (рис. 2.5а), имеет место равновесие. Если же силы 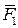и 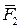сжимают нить (рис. 2.5б), то система утрачивает равновесие.

Лемма. Внутренние силы, действующие в данном абсолютно твердом теле, образуют уравновешенную систему сил и на условия равновесия тела не влияют.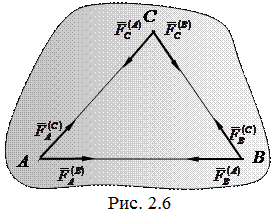

Доказательство. Внутренние силы, приложенные в данном твердом теле, можно представить разложенными на попарно уравновешенные силы. Рассмотри три точки тела: А, В, и С, и обозначим внутренние силы как показано на рис. 2.6 В силу аксиомы равенства действия и противодействия имеем

.

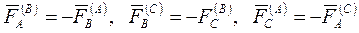На основании аксиомы 1 система внутренних сил данного тела, приложенных к трем его точкам, эквивалентна нулю:

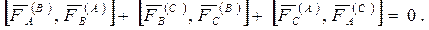
Дата добавления: 2014-11-29