Примеры решения задач. Тело движется прямолинейно со скоростью v, пропорциональной квадрату времени t

Задача 1.19

Тело движется прямолинейно со скоростью v, пропорциональной квадрату времени t. Установить зависимость между пройденным путем S и временем t, если известно, что в начальный момент времени (при t = 0) пройденный телом путь S (0) = S₀.

Дано: v ~ t ²; S (0) = S ₀.

Найти: S (t).

Решение. Поусловию задачи

v ~ t ². (1)

Чтобы вместо знака пропорциональности «~» поставить знак равенства,введем коэффициент k. Тогда

v=kt ². (2)

По определению скорость v — первая производная пути S по времени t, т. е. путь S, время t и скорость v связаны дифференциальным уравнением

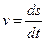. (3)

Приравняем правые части выражений (2) и (3). Получим

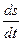= kt². (4)

Соотношение (4) является дифференциальным уравнением первого порядка с разделяющимися переменными, так как его можно записать в виде

dS = kt²dt. (5)

Проинтегрировав обе части равенства (5), получим общее решение дифференциального уравнения (4)

∫dS = ∫kt²dt S (t) = ∫kt²dt = 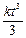+ C. (6)

В начальный момент времени S = S ₀, поэтому, подставив в общее решение (6) значения времени t = 0 и пути S = S ₀, найдем значение постоянной интегрирования С

S (0) = S ₀ = 0 + С. (7)

Тогда С = S₀. Найденное значение С подставим в общее решение (6) и получим частное решение

S (t) = 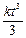+ S ₀. (8)

Ответ: зависимость пройденного телом пути от времени имеет вид

S (t) = 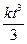+ S _0.

Задача 1.20

Найти общее решение дифференциального уравнения

2у" + 5у' + 2у = 0. (1)

Решение. Заданное уравнение — линейное однородное дифференциальное уравнение с постоянными коэффициентами. Для его решения составим характеристическое уравнение

2k² + 5k + 2 = 0. (2)

Найдем корни уравнения (2)

.

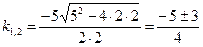Тогда k₁= - 2 и k₂ = -0,5. Так как корни действительные различные, тогда частные решения уравнения (1) имеют вид у ₁ = 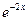и у ₂ = 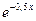, и общее решение уравнения (1) запишется как

у = C ₁ 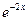+ C ₂ .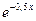

Ответ: у = C ₁ 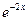+ C ₂ .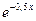

Задача 1.21

Найти частное решение дифференциального уравнения

у"-2у' + у = 0, (1)

удовлетворяющее начальным условиям у( 0 ) = 4, у'( 0 ) = 2.

Решение. Данное уравнение — линейное однородное дифференциальное уравнение с постоянными коэффициентами. Для его решения составим характеристическое уравнение и найдем его корни

k ²-2 k +1 = 0, (k - 1)² = 0, (k - 1) = 0, k ₁₂= 1.

Так как корни действительные, согласно таблице 3, то частные решения данного уравнения имеют вид у ₁ =е^х и у ₂ = хе^х, а общее решение уравнения (1) запишется как

у=С ₁ е^х+С ₂ хе^х = е^х (С ₁ + С ₂ х). (2)

Найдем у', дифференцируя по х выражение (2):

у' = (е^х (С ₁ + С ₂ х)) ' = (е^х)' (С ₁+ С ₂ х) + е^х (С ₁+ С ₂ х) ' =

= е^х (С ₁+ С ₂ х)+ е^х (0 + С ₂) =

= е^х (С ₁ + С ₂ х+ С ₂).

(при нахождении производной пользовались формулами (3) и (8) из таблицы производных с. 33—34 и правилом дифференцирования произведения двух функций — формулой (2.15) с. 34)

Итак,

y'= е^х (С ₁ + C ₂ x+C ₂). (3)

Для определения частного решения уравнения (1) в равенства (2) и (3) подставим начальные условия:

у (0) = С ₁ е ⁰ + С ₂ 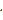0 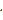е ⁰=4, (2*)

y' (0) = е⁰(С ₁ + C ₂ 0 + C ₂) = 2. (3*)

Получим систему двух уравнений

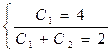
из которой определяем постоянные С ₁ = 4 и = -2.

Подставив эти значения в общее решение (2) уравнения (1), найдем частное решение уравнения (1):

у = 4 е^х - 2 хе^х. (4)

Ответ: у = 4 е^х - 2 хе^х.

Дата добавления: 2014-11-29