Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Уравнение вида

А ₀ у"+ а ₁ у' + а ₂ y = f (x), (1.74)

где а ₀, а ₁ а ₂ — постоянные коэффициенты, а f (х) — непрерывная функция, называется линейным неоднородным дифференциальным уравнениемвторого порядка с постоянными коэффициентами. Ниже ограничимся рассмотрением случая, когда правая часть уравнения (1.74) имеет вид

.

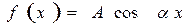Это уравнение вынужденных механических колебаний, которые предстоит изучать в разделе «Механические колебания».

Уравнение с теми же коэффициентами a ₀ a ₁, a ₂, но с правой частью, равной нулю

a ₀ у "+ a₁ у ' + a ₂ y = 0, (1.75)

называется однородным уравнением, соответствующим неоднородному уравнению (1.74). Для линейных неоднородных уравнений имеют место следующие теоремы, с помощью которых отыскиваются их общие решения.

Теорема 1. Если известно какое-либо частное решение у* неоднородного уравнения (1.74), то его общее решение у есть сумма частного решения у* и общего решения Y соответствующего однородного уравнения (1.75), т. е.

y = y*+Y. (1.76)

Теорема 2. Если правая часть линейного уравнения с постоянными коэффициентами может быть представлена в виде

,

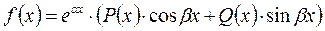где Р (х)и Q (х)- многочлены и 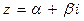не является корнем характеристического уравнения, то существует частное решение вида

,

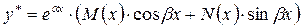где М (x)и N (x)— многочлены той же степени, что и P(x), Q(x).

Задача 1.22

Найти общее решение дифференциального уравнения

у " - 5 у ' + 6 у = 13sin3 x (1)

Решение. Данное уравнение - линейное неоднородное дифференциальное уравнение с постоянными коэффициентами. Для его решения составим характеристическое уравнение и найдем его корни.

k ² - 5 k +6 = 0

(k - 2)(k - 3) = 0

k ₁ + = 2, k ₂= 3,

Так как корни действительные различные,, общее решение Y однородного дифференциального уравнения

у"- 5 у' + 6 у= 0(2)

имеет вид

. (3)

Правую часть уравнения (1) можно записать в виде

.

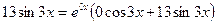Здесь α = 0, β = 3, Р (x)= 0, Q (x) = 13 (многочлен нулевой степени). Так как число

z = α + β = 3 i не является корнем характеристического уравнения, согласно теореме 2, частное решение уравнения (1) ищем в виде

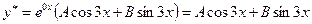. (4)

Найдем

(5)

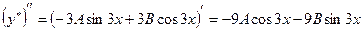. (6)

Подставив (4)и (5) в уравнение (1), получим тождество

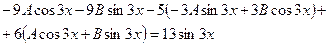(7)

или после преобразований

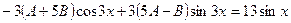. (8)

Приравняем коэффициенты пр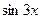и и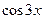

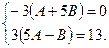
Решив полученную систему уравнений, получим А = 5/6 и В = - 1/6.

Найденные коэффициенты подставим в (6):

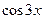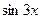у* = 5/6 - 1/6 . (9)

Т.о., найден вид частного решения заданного уравнения (1).

Согласно теореме 1, общее решение уравнения (1) имеет вид

у = y* + Y.

Подставив в это соотношение формулы (3) и (9), получим общее, решение уравнения (1):

у = 5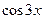/6 - l/6 +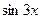

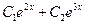
Ответ: у = 5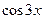/6 - l/6 + .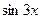

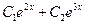Вывод

Понятия, рассмотренные в данной главе, часто используются при изучении теоретической механики. Например, вектор и действия с ним – это основа статики: сосредоточенная сила. Не представляя, как вектор проецируется на оси, невозможно составить уравнения равновесия, то есть невозможно решить ни одной задачи из раздела статики. В кинематике также очень часто используется векторная алгебра. Все кинематические характеристики являются векторами или их проекциями. Сложное движение точки и тела легче изучать, зная правила векторного и скалярного перемножения векторов. В динамике кроме векторных сил широко применяются правила дифференцирования и интегрирования. На этом основано решение основной задачи динамики. При изучении колебательного движения необходимо иметь представление о правилах составления и решения дифференциальных уравнений.

Контрольные вопросы

1. Сформулируйте понятие вектора.

2. Чем отличается векторное произведение векторов от скалярного?

3. Что такое проекция вектора на ось и плоскость?

4. Как согласуются координаты вектора с его длиной?

5. Укажите физический смысл скалярного произведения векторов.

6. Укажите физический смысл векторного произведения векторов.

7. Укажите отличия дифференциала от производной?

8. Укажите физический смысл производной.

9. Сформулируйте основные правила взятия производной: производная суммы и произведения, степенной функции.

10. Чем отличается определённый интеграл от неопределённого?

11. Укажите физический смысл интеграла.

12. Определите дифференциальное уравнение.

13. Сформулируйте правила нахождения общего и частного решений дифференциальных уравнений.

ГЛАВА 2 СТАТИКА

Дата добавления: 2014-11-29