Система сходящихся сил. Сложение сил

Статика как учение о равновесии твердых тел под действием приложенных к ним сил содержит две основные задачи:

1) замена данной системы сил ей эквивалентной, и

2) вывод общих условий равновесия твердых тел.

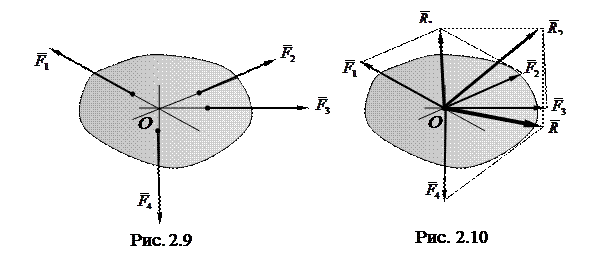Сходящейся называется система сил, линии, действия которых пересекаются в одной точке.

Рассмотрим пространственную систему сходящихся сил (рис. 2.9). На основании аксиомы 2 силы 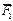, ,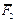..., можно перенести вдоль линии их действия в точку пересечения О (рис. 2.9). Складывая силы последовательно по две (попарно) по правилу параллелограмма, приходим к результирующей силе, которую называют равнодействующей системы сходящихся сил (рис. 2.10):

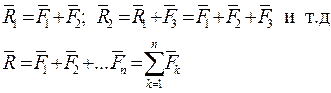(2.4)

Таким образом, равнодействующая равна геометрической сумме сил системы и приложена в точке их пересечения, называемой точкой схода (т. О).

Силы можно складывать и по правилу многоугольника (рис. 2.11). Присоединяя к концу силы 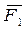силу 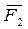, к концу силы силу 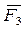и т.д., строим силовой многоугольник. Равнодействующую получим, проводя вектор из точки схода О в конец последнего вектора .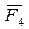

Если система сил уравновешена, то силовой многоугольник должен быть замкнут (рис. 2.12), а равнодействующая, следовательно, равна нулю:

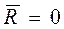(2.5)

Из выражения (2.4) следует, что для уравновешенной системы сил

. (2.6)

Условия (2.5), и (2.6) служат условиями равновесия системы сходящихся сил в векторной форме.

Теорема о равновесии трех непараллельных сил. Если абсолютно твердое тело находится в равновесии под действием трех непараллельных сил, расположенных в одной плоскости, то линии действия этих сил пересекаются в одной точке.

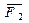Докажем теорему о равновесии трех непараллельных сил. Перенесем силы силу (рис. 2.13 а)) в точку О пересечения линий их действия и сложим:

.

Теперь можно считать, что на тело действуют две силы 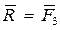, и согласно аксиоме 2 они составляют

уравновешенную систему, если направлены по общей линии действия в разные стороны. Следовательно, линия действия силы 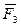должна также проходить через точку О.

Уравновешенная система из трех сил представляет собой замкнутый треугольник (рис. 2.13, б). Зная три элемента этого треугольника (сторону и два прилежащих угла или две стороны и угол между ними), можно, используя теоремы и формулы тригонометрии, определить другие его элементы, например неизвестные силы.

Задача 2.1

Поворотный кран (рис. 2.14, а))находится в равновесии под действием силы тяжести груза Q - 12 кН. Размеры крана: H = 4м, L = 3м. Определить опорные реакции в опорах А и В.

Решение. В точке А имеем цилиндрический шарнир, и направление реакции следовательно, известно. Продолжив ее линию действия до пересечения с линией действия силы , получим точку О, через которую, очевидно, должна пройти реакция 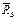. Построим замкнутый силовой треугольник. Изобразив в некотором масштабе силу , через один конец этого вектора проводим линию, параллельную реакции , а через другой - линию, параллельную реакции 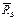(рис. 2.14, б).

Из подобия треугольника AОВ силовому треугольнику имеем

,

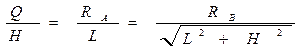отсюда .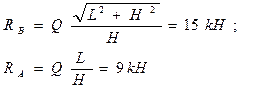

Задача 2.2

Балка АВ длиной 2м (рис. 2.15, а) опирается на неподвижный А и подвижный В шарниры и нагружена силой , приложенной к середине балки под углом 45⁰ к ней. Определить реакции опор А и В.

Решение. Так, как направление реакции 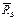известно (она перпендикулярна плоскости качения), проводим линии действия сил 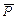и 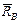до их взаимного пересечения в точке О. Очевидно, что через эту точку должна пройти и линия действия реакции . Изобразим замкнутый силовой треугольник. Покажем в некотором масштабе силу 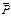(рис. 2.15, б). Через один конец вектора силы 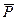проведем линию действия реакции , через другой конец вектора силы - линию, параллельную аправлению реакции .

Расставим векторы 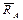и так, чтобы получился замкнутый треугольник сил. Из треугольника имеем соотношение (по теореме синусов):

,

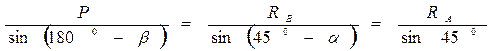Откуда .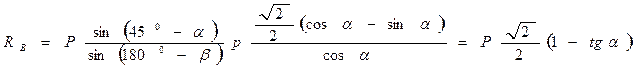

Из рис. 2.15,а) имеем ВО=ВС=АС =1м; ;

.

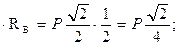
Дата добавления: 2014-11-29