Пример. Общее и частное решение дифференциального уравнения

Общее и частное решение дифференциального уравнения

Дифференциальное уравнение, его порядок.

Дифференциальные уравнения

При решении задач по теоретической механике часто возникают уравнения, называемые дифференциальными. Такими являются уравнения движения тел, составленные по второму закону Ньютона (если хотя бы одна из сил, действующих на тело, зависит от времени), уравнения незатухающих, затухающих и вынужденных колебаний.

Метод решения дифференциального уравнения определяется видом уравнения; огромное число таких уравнений имеет только численное решение, в некоторых случаях решение дифференциального уравнения может подсказать сам характер исследуемого физического явления.

Рассмотрим виды дифференциальных уравнений, наиболее часто возникающих при описании физических процессов.

Дифференциальным называется уравнение, связывающее независимую переменную х, неизвестную функцию у = f (x)и ее производные у', у"..., у ^{( n )}.

Символически дифференциальное уравнение можно записать в виде

F (x,y,y',y",..., у⁽ⁿ⁾) = 0. (1.54)

Порядок наивысшей производной, входящей в уравнение, называется порядком дифференциального уравнения.

Например, второй закон Ньютона в общем случае есть дифференциальное уравнение второго порядка, так как ускорение, входящее в это уравнение, — вторая производная координат по времени.

Решением дифференциального уравнения называется всякая функция у = f (x), которая при подстановке в уравнение (4.1) превращает его в тождество.

Уравнение

ху'+у= 0(1.55)

является дифференциальным уравнением первого порядка, так как содержит производную первого порядка у'. Функция

y=1/х (1.56)

является его решением. Действительно, подставляя у = 1 / х и у' = - 1/ 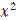в уравнение (1.55), получаем

х (-1 / х ²) + 1/ х = 0. (1.57)

Функция у=1 / х обращает уравнение (1.55) в тождество, т. е. является его решением. Есть и другие решения: у = 2 /х, у = 5 /х, а также любая функция вида

y = С/х, (1.58)

где C — произвольная постоянная.

Действительно,

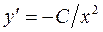(1.59)

и подстановка выражений (1.58) и (1.59) в уравнение (1.55) дает

x (-С/х²)+ С/x = 0, (1.60)

т. е. также превращает его в тождество. Оказывается, решений много, причем выражение (1.58) содержит наряду с переменной x параметр С.

Общим решением уравнения (1.54) называется функция

y = φ(x,C), (1.61)

которая зависит от x и от произвольной постоянной С и обладает следующими свойствами:

1) удовлетворяет дифференциальному уравнению (1.54) при любом конечном значении постоянной C,

2) при любом начальном условии у (x₀) = у₀, можно найти такое значение С = С₀, что функция y = φ(x, С ₀) удовлетворяет данному начальному условию.

Частным решением дифференциального уравнения называется функция

y = φ(x,C ₀), (1.62)

которая получается из общего решения y = φ(x, C), если произвольной постоянной C придать определенное значение C = С ₀.

Геометрически общее решение у = f (x, С)уравнения (1.54) представляет собой семейство кривых на координатной плоскости, зависящее от одной произвольной постоянной С.

Кривая семейства, проходящая через точку М₀ (x₀, у₀), представляет собой график частного решения y = φ(x, С₀) при начальном условии у (x₀) = у₀.

Дата добавления: 2014-11-29